Design of 2D Planar Sparse Binned Arrays Based on the Coarray Analysis

Abstract

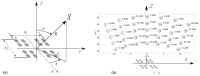
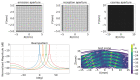
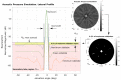
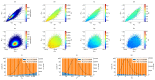
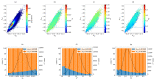
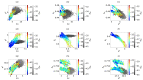
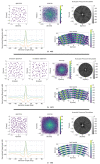
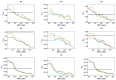
The analysis of the beampattern is the base of sparse arrays design process. However, in the case of bidimensional arrays, this analysis has a high computational cost, turning the design process into a long and complex task. If the imaging system development is considered a holistic process, the aperture is a sampling grid that must be considered in the spatial domain through the coarray structure. Here, we propose to guide the aperture design process using statistical parameters of the distribution of the weights in the coarray. We have studied three designs of sparse matrix binned arrays with different sparseness degrees. Our results prove that there is a relationship between these parameters and the beampattern, which is valuable and improves the array design process. The proposed methodology reduces the computational cost up to 58 times with respect to the conventional fitness function based on the beampattern analysis.

Keywords: beamforming; sparse arrays; ultrasonic imaging.

Figure 1

(a) Coordinate system used for beampattern simulation; (b) test scenario used to evaluate the imaging capabilities of the apertures.

Figure 2

Projection of the $$\mathrm{FMC}\left(\overrightarrow{\chi }\right)$$ when the reflector is located at ($$R=100\mathrm{mm},\theta =0^{\circ },\varphi =0^{\circ }$$). If $$\overrightarrow{\chi }=(R=100\mathrm{mm}$$, $$\theta =0^{\circ },\varphi =0^{\circ })$$ is in the reflector: (a) coarray of a full array; (b) coarray of minimum redundancy array; (c) coarray of sparse array. If $$\overrightarrow{\chi }=(R=100\mathrm{mm},\theta ={12}^{\circ },\varphi ={80}^{\circ })$$ is out of the reflector: (d) coarray of a full array; (e) coarray of minimum redundancy array; (f) coarray of sparse array.

Figure 3

Sparse aperture solution to solve a minimum redundancy coarray. In the top, emission and reception apertures are presented with the resultant coarray. In the bottom-left, the beampattern in the x-axis (R = 100 mm, $$\varphi =0^{\circ }$$,) is presented at different steering angles ( $$0^{\circ }$$ blue, $${10}^{\circ }$$ yellow, $${20}^{\circ }$$ green and $${30}^{\circ }$$ red). In the bottom-right the image generated by this array from the scenario presented in Figure 1b.

Figure 4

Elements used to evaluate the beampattern simulation. The beampattern is simulated in a semi-sphere ($$\theta \in [-{90}^{\circ }:\Delta \alpha :+{90}^{\circ }]$$, $$\varphi \in [0^{\circ }:\Delta \alpha :{180}^{\circ }]$$, $$\Delta \alpha =\frac{1}{2}\Delta {\theta }_{-6\mathrm{dB}}$$). The three lateral profiles are composed of the semi-sphere by obtaining, at each elevation angle, the maximum, the mean and the minimum. The peak sidelobe $$\left(A_{pk}\right)$$ and the mainlobe width $$\Delta {\theta }_{A_{pk}}$$ are identified. The mean value of the sidelobes is $$A_{mn}$$. Furthermore, finally, the $$0.5\%$$ percentile of the maximum sidelobes is identified and evaluated by its mean value ($$A_{m5}$$).

Figure 5

Results of 100,000 random cases of configuration 100I. In the first row, the apertures are presented in a $$A_{m5}$$ vs. $$A_{pk}$$ map, (a) population, (b) $$S_a$$, (c) $${\sigma }^2$$ and (d) $$Ku$$. In the second row, the apertures are presented in $$A_{m5}$$ vs. $$A_{mn}$$ map, (e) population, (f) $$S_a$$, (g) $${\sigma }^2$$ and (h) $$ku$$. In the third row, the distribution of cases against the coarray parameters are presented, marking the proportion of cases that fulfill the $$T{H}_{A_{m5}}$$ threshold, (i) $$S_a$$, (j) $${\sigma }^2$$ and (k) $$Ku$$.

Figure 6

Results of 100,000 random cases of configuration 100V. In the first row, the apertures are presented in $$A_{m5}$$ vs. $$A_{pk}$$ map, (a) population, (b) $$S_a$$, (c) $${\sigma }^2$$ and (d) $$Ku$$. In the second row, the distribution of cases against the coarray parameters are presented, marking the proportion of case that fulfill the $$T{H}_{A_{m5}}$$ threshold, (e) $$S_a$$, (f) $${\sigma }^2$$ and (g) $$Ku$$.

Figure 7

Results of 50,000 random cases of configuration 196I. In the first row, the apertures are presented in $$A_{m5}$$ vs. $$A_{pk}$$ map, (a) population, (b) $$S_a$$, (c) $${\sigma }^2$$ and (d) $$Ku$$. In the second row, the distribution of cases against the coarray parameters are presented, marking the proportion of case that fulfill the $$T{H}_{A_{m5}}$$ threshold, (e) $$S_a$$, (f) $${\sigma }^2$$ and (g) $$Ku$$.

Figure 8

In color, the values of $$A_{m5}$$ reached by the candidates apertures in the search process. In gray, the values of $$A_{m5}$$ obtained with 100,000 random apertures. Configuration 100I: (a), $${\sigma }^2\times Ku$$, (b), $$S_a\times Ku$$, and (c) $$S_a\times {\sigma }^2$$. Configuration 100V: (d), $${\sigma }^2\times Ku$$, (e), $$S_a\times Ku$$, and (f) $$S_a\times {\sigma }^2$$. Configuration 196I: (g), $${\sigma }^2\times Ku$$, (h), $$S_a\times Ku$$, and (i) $$S_a\times {\sigma }^2$$ for configuration 196I.

Figure 9

Coarray-based fitness function. Each row analyses the evolution of the dynamic range in one specific configuration. For $$100\mathrm{I}$$: (a) $$A_{m5}$$, (d) $$A_{mn}$$, (g) $$A_{pk}$$. For $$100\mathrm{V}$$: (b) $$A_{m5}$$, (e) $$A_{mn}$$, (h) $$A_{pk}$$. For $$196\mathrm{I}$$: (c) $$A_{m5}$$, (f) $$A_{mn}$$, (i) $$A_{pk}$$. For each configuration three different evolution processes are presented (colors blue, orange and green). In the figures where $$A_{pk}$$ or $$A_{m5}$$ are presented, the threshold line $$T{H}_{A_{m5}}$$ has been indicated.

Figure 10

Optimization with coarray based fitness function. Best results for configurations (a) $$100\mathrm{I}$$, (b) $$100\mathrm{V}$$ and (c) $$196\mathrm{I}$$. In each figure are presented: emission (and reception for $$100\mathrm{V}$$) apertures; coarray matrix representation; acoustic field in the semi-sphere; maximum (blue), mean (green) and minimum (red) lateral profile at each elevation angle; and image resulting from the test scenario.

Figure 11

Combined fitness function. Each row analyses the evolution of the dynamic range in one specific configuration. For $$100\mathrm{I}$$: (a) $$A_{m5}$$, (d) $$A_{mn}$$, (g) $$A_{pk}$$. For $$100\mathrm{V}$$: (b) $$A_{m5}$$, (e) $$A_{mn}$$, (h) $$A_{pk}$$. For $$196\mathrm{I}$$: (c) $$A_{m5}$$, (f) $$A_{mn}$$, (i) $$A_{pk}$$. For each configuration three different evolution processes are presented (colors blue, orange and green). In the figures where $$A_{pk}$$ or $$A_{m5}$$ are presented, the threshold line $$T{H}_{A_{m5}}$$ has been indicated.

Figure 12

Optimization with combined fitness function. Best results for configurations (a) 100I, (b) 100V and (c) 196I. In each figure are presented: emission (and reception for 100V) apertures; coarray matrix representation; acoustic field in the semi-sphere; and, maximum (blue), mean (green) and minimum (red) lateral profile at each elevation angle; and image resulting from the test scenario.