A Method for Estimating the Deposition Density of Fallout on the Ground and on Vegetation from a Low-yield, Low-altitude Nuclear Detonation
- PMID: 34898515
- PMCID: PMC8677616
- DOI: 10.1097/HP.0000000000001496
A Method for Estimating the Deposition Density of Fallout on the Ground and on Vegetation from a Low-yield, Low-altitude Nuclear Detonation
Abstract
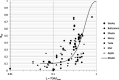
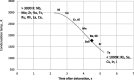
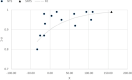
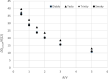
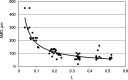
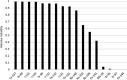
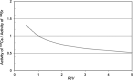
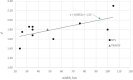
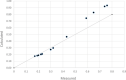
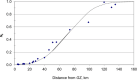
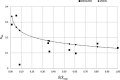
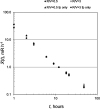
This paper describes a relatively simple model developed from observations of local fallout from US and USSR nuclear tests that allows reasonable estimates to be made of the deposition density (activity per unit area) on both the ground and on vegetation for each radionuclide of interest produced in a nuclear fission detonation as a function of location and time after the explosion. In addition to accounting for decay rate and in-growth of radionuclides, the model accounts for the fractionation (modification of the relative activity of various fission and activation products in fallout relative to that produced in the explosion) that results from differences in the condensation temperatures of the various fission and activation products produced in the explosion. The proposed methodology can be used to estimate the deposition density of all fallout radionuclides produced in a low yield, low altitude fission detonation that contribute significantly to dose. The method requires only data from post-detonation measurements of exposure rate (or beta or a specific nuclide activity) and fallout time-of-arrival. These deposition-density estimates allow retrospective as well as rapid prospective estimates to be made of both external and internal radiation exposure to downwind populations living within a few hundred kilometers of ground zero, as described in the companion papers in this volume.
Copyright © 2021 Written work prepared by employees of the Federal Government as part of their official duties is, under the U.S. Copyright Act, a “work of the United States Government” for which copyright protection under Title 17 of the United States Code is not available. As such, copyright does not extend to the contributions of employees of the Federal Government.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures











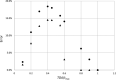
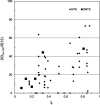


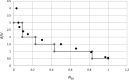
Similar articles
-
A Methodology for Calculation of Internal Dose Following Exposure to Radioactive Fallout from the Detonation of a Nuclear Fission Device.Health Phys. 2022 Jan 1;122(1):84-124. doi: 10.1097/HP.0000000000001503. Health Phys. 2022. PMID: 34898517 Free PMC article.
-
A Methodology for Estimating External Doses to Individuals and Populations Exposed to Radioactive Fallout from Nuclear Detonations.Health Phys. 2022 Jan 1;122(1):54-83. doi: 10.1097/HP.0000000000001504. Health Phys. 2022. PMID: 34898516 Free PMC article.
-
Dose Estimation for Exposure to Radioactive Fallout from Nuclear Detonations.Health Phys. 2022 Jan 1;122(1):1-20. doi: 10.1097/HP.0000000000001501. Health Phys. 2022. PMID: 34898514 Free PMC article.
-
Historical overview of atmospheric nuclear weapons testing and estimates of fallout in the continental United States.Health Phys. 2002 May;82(5):591-608. doi: 10.1097/00004032-200205000-00007. Health Phys. 2002. PMID: 12003011 Review.
-
Review of methods of dose estimation for epidemiological studies of the radiological impact of nevada test site and global fallout.Radiat Res. 2006 Jul;166(1 Pt 2):209-18. doi: 10.1667/RR3172.1. Radiat Res. 2006. PMID: 16808609 Review.
Cited by
-
Inter-agency perspective: Translating advances in biomarker discovery and medical countermeasures development between terrestrial and space radiation environments.Life Sci Space Res (Amst). 2022 Nov;35:9-19. doi: 10.1016/j.lssr.2022.06.004. Epub 2022 Jun 14. Life Sci Space Res (Amst). 2022. PMID: 36336375 Free PMC article.
-
A Historical Survey of Key Epidemiological Studies of Ionizing Radiation Exposure.Radiat Res. 2024 Aug 1;202(2):432-487. doi: 10.1667/RADE-24-00021.1. Radiat Res. 2024. PMID: 39021204 Free PMC article. Review.
-
A Methodology for Calculation of Internal Dose Following Exposure to Radioactive Fallout from the Detonation of a Nuclear Fission Device.Health Phys. 2022 Jan 1;122(1):84-124. doi: 10.1097/HP.0000000000001503. Health Phys. 2022. PMID: 34898517 Free PMC article.
-
A Methodology for Estimating External Doses to Individuals and Populations Exposed to Radioactive Fallout from Nuclear Detonations.Health Phys. 2022 Jan 1;122(1):54-83. doi: 10.1097/HP.0000000000001504. Health Phys. 2022. PMID: 34898516 Free PMC article.
-
Parameter Values for Estimation of Internal Doses from Ingestion of Radioactive Fallout from Nuclear Detonations.Health Phys. 2022 Jan 1;122(1):236-268. doi: 10.1097/HP.0000000000001493. Health Phys. 2022. PMID: 34898519 Free PMC article.
References
-
- Baurmash L, Neel JW, Vance WK, III, Mork HM, Larson KH. Distribution and characterization of fallout and airborne activity from 10 to 160 miles from ground zero, spring 1955. Los Angeles, CA: University of California; WT-1178; 1958.
-
- Beck HL. Exposure rate conversion factors for radionuclides deposited on the ground. New York: US Department of Energy Environmental Measurements Laboratory; EML-378; 1980.
-
- Beck HL, Krey PW. Radiation exposure in Utah from Nevada nuclear tests. Science 220:18–24; 1983. - PubMed
-
- Beck HL, Anspaugh LR. Development of the County Data Base: estimates of exposure rates and times of arrival of fallout in the ORERP Phase II Area: comparison with cumulative deposition-density estimates based on analyses of retrospective and historical soil samples. Las Vegas, NV: US Department of Energy; DOE/NV-320; 1991.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

