Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Feb;45(3):1632-1639.
doi: 10.1002/mma.7878. Epub 2021 Oct 12.

R 0 estimation for COVID-19 pandemic through exponential fit

Zheng Mingliang  1 , Theodore E Simos  2   3   4   5   6 , Charalampos Tsitouras  7
Affiliations

R 0 estimation for COVID-19 pandemic through exponential fit

Zheng Mingliang et al. Math Methods Appl Sci. 2022 Feb.

Abstract

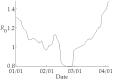
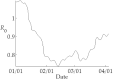
We provide an easy and accurate method for approximating the reproduction number R 0 defined in an SIR epidemic model. At first, we present a formula extracting the exact R 0 in case of constant rates of infection and recovery assumed in an SIR model. Then, we proceed proposing an exponential fitting to various data taken from the real-world epidemics. Certain applications for current COVID outbreak are considered, and figures describing the fluctuation of R 0 in various countries are given.

Keywords: COVID‐19 outbreak; SIR epidemic model; exponential fitting; initial value problem.

PubMed Disclaimer

Figures

FIGURE 1
FIGURE 1
Brazil: R 0 estimation between January 1, 2021 until April 4, 2021
FIGURE 2
FIGURE 2
Canada: R 0 estimation between January 1, 2021 until April 4, 2021
FIGURE 3
FIGURE 3
Germany: R 0 estimation between January 1, 2021 until April 4, 2021
FIGURE 4
FIGURE 4
Israel: R 0 estimation between January 1, 2021 until April 4, 2021
FIGURE 5
FIGURE 5
Italy: R 0 estimation between January 1, 2021 until April 4, 2021
FIGURE 6
FIGURE 6
Russia: R 0 estimation between January 1, 2021 until April 4, 2021
See this image and copyright information in PMC

References

    1. Kermack WO, McKendrick AG. Contributions to the mathematical theory of epidemics—I. Proc R Soc A. 1927;115:700‐721. - PubMed
    1. Beckett SJ, Dominguez‐Mirazo M, Lee S, Andris C, Weitz JS. Spread of COVID‐19 through Georgia, USA. Near‐term projections and impacts of social distancing via a meta population model. 10.1101/2020.05.28.20115642; 2020. - DOI
    1. Korsbo N, Jonsson H. Its about time: analysing simplifying assumptions for modelling multi‐step pathways in systems biology. PLoS Comput Biol. 2020;16:e1007982. - PMC - PubMed
    1. Weitz JS, Beckett SJ, Coenen AR, et al. Modeling shield immunity to reduce COVID‐19 epidemic spread. Nat Med. 2020;26:849‐854. - PMC - PubMed
    1. Medvedev MA, Simos TE, Tsitouras C. Fitted modifications of Runge‐Kutta pairs of orders 6(5). Math Meths Appl Sci. 2018;41:6184‐6194.

LinkOut - more resources