Fractional Chern insulators in magic-angle twisted bilayer graphene
- PMID: 34912084
- PMCID: PMC8674130
- DOI: 10.1038/s41586-021-04002-3
Fractional Chern insulators in magic-angle twisted bilayer graphene
Abstract
Fractional Chern insulators (FCIs) are lattice analogues of fractional quantum Hall states that may provide a new avenue towards manipulating non-Abelian excitations. Early theoretical studies1-7 have predicted their existence in systems with flat Chern bands and highlighted the critical role of a particular quantum geometry. However, FCI states have been observed only in Bernal-stacked bilayer graphene (BLG) aligned with hexagonal boron nitride (hBN)8, in which a very large magnetic field is responsible for the existence of the Chern bands, precluding the realization of FCIs at zero field. By contrast, magic-angle twisted BLG9-12 supports flat Chern bands at zero magnetic field13-17, and therefore offers a promising route towards stabilizing zero-field FCIs. Here we report the observation of eight FCI states at low magnetic field in magic-angle twisted BLG enabled by high-resolution local compressibility measurements. The first of these states emerge at 5 T, and their appearance is accompanied by the simultaneous disappearance of nearby topologically trivial charge density wave states. We demonstrate that, unlike the case of the BLG/hBN platform, the principal role of the weak magnetic field is merely to redistribute the Berry curvature of the native Chern bands and thereby realize a quantum geometry favourable for the emergence of FCIs. Our findings strongly suggest that FCIs may be realized at zero magnetic field and pave the way for the exploration and manipulation of anyonic excitations in flat moiré Chern bands.
© 2021. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures
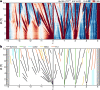



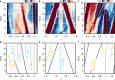


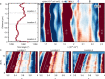
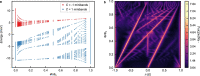
References
-
- Regnault N, Bernevig BA. Fractional Chern insulator. Phys. Rev. X. 2011;1:021014. - PubMed
Publication types
LinkOut - more resources
Full Text Sources

