Planning Fail-Safe Trajectories for Space Robotic Arms
- PMID: 34917652
- PMCID: PMC8671041
- DOI: 10.3389/frobt.2021.710021
Planning Fail-Safe Trajectories for Space Robotic Arms
Abstract
A frequent concern for robot manipulators deployed in dangerous and hazardous environments for humans is the reliability of task executions in the event of a joint failure. A redundant robotic manipulator can be used to mitigate the risk and guarantee a post-failure task completion, which is critical for instance for space applications. This paper describes methods to analyze potential risks due to a joint failure, and introduces tools for fault-tolerant task design and path planning for robotic manipulators. The presented methods are based on off-line precomputed workspace models. The methods are general enough to cope with robots with any type of joint (revolute or prismatic) and any number of degrees of freedom, and might include arbitrarily shaped obstacles in the process, without resorting to simplified models. Application examples illustrate the potential of the approach.
Keywords: fail-safe trajectories; fault-tolerant manipulators; manipulation planning; robotic arms; space manipulator.
Copyright © 2021 Porges, Leidner and Roa.
Conflict of interest statement
OP was employed by the company Agile Robots The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures
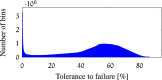
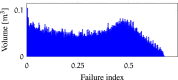
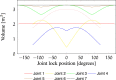
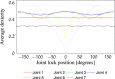




References
-
- Alkmarkhi A., Maciejewski A. A. (2019). Maximizing the Size of Self-Motion Manifolds to Improve Robot Fault-Tolerance. IEEE Robotics Automation Lett. 4, 2653–2660. 10.1109/LRA.2019.2913994 - DOI
-
- Burdick J. W. (1989). On the Inverse Kinematics of Redundant Manipulators: Characterization of the Self-Motion Manifolds, in IEEE Int. Conf. Robotics and Automation, 264–270. 10.1109/ROBOT.1989.99999 - DOI
-
- Diankov R. (2010). Automated Construction of Robotic Manipulation Programs, (Pittsburgh, Pennsylvania: Carnegie Mellon University; ). Ph.D. thesis. ISBN: 978-1-124-53547-0.
-
- Ellery A., Kreisel J., Sommer B. (2008). The Case for Robotic On-Orbit Servicing of Spacecraft: Spacecraft Reliability Is a Myth. Acta Astronautica 63, 632–648. 10.1016/j.actaastro.2008.01.042 - DOI
-
- Jaekel S., Lampariello R., Panin G., Sagardia M., Brunner B., Porges O., et al. (2015). Robotic Capture and De-orbit of a Heavy, Uncooperative and Tumbling Target in Low Earth Orbit, in Workshop on Advanced Space Technologies for Robotics and Automation - ASTRA.
LinkOut - more resources
Full Text Sources

