Implicit Solvation Methods for Catalysis at Electrified Interfaces
- PMID: 34928131
- PMCID: PMC9227731
- DOI: 10.1021/acs.chemrev.1c00675
Implicit Solvation Methods for Catalysis at Electrified Interfaces
Abstract
Implicit solvation is an effective, highly coarse-grained approach in atomic-scale simulations to account for a surrounding liquid electrolyte on the level of a continuous polarizable medium. Originating in molecular chemistry with finite solutes, implicit solvation techniques are now increasingly used in the context of first-principles modeling of electrochemistry and electrocatalysis at extended (often metallic) electrodes. The prevalent ansatz to model the latter electrodes and the reactive surface chemistry at them through slabs in periodic boundary condition supercells brings its specific challenges. Foremost this concerns the difficulty of describing the entire double layer forming at the electrified solid-liquid interface (SLI) within supercell sizes tractable by commonly employed density functional theory (DFT). We review liquid solvation methodology from this specific application angle, highlighting in particular its use in the widespread ab initio thermodynamics approach to surface catalysis. Notably, implicit solvation can be employed to mimic a polarization of the electrode's electronic density under the applied potential and the concomitant capacitive charging of the entire double layer beyond the limitations of the employed DFT supercell. Most critical for continuing advances of this effective methodology for the SLI context is the lack of pertinent (experimental or high-level theoretical) reference data needed for parametrization.
Conflict of interest statement
The authors declare no competing financial interest.
Figures



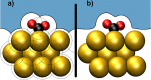

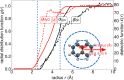
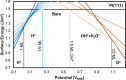

 around the PZC for a model Li(110) electrode
in implicit ethylene carbonate (EC) solvent (εr =
89.9). The parabolic variation nicely reflects the Taylor expansion
of eq 45 and allows
fitting of the interfacial capacitance. (left) Variation as a function
of the bulk permittivity employed in the implicit solvation model.
(right) Variation as a function of the threshold charge density (called nc) employed to define the solvation cavity.
Reproduced from ref (402). Copyright 2015 American Chemical Society.
around the PZC for a model Li(110) electrode
in implicit ethylene carbonate (EC) solvent (εr =
89.9). The parabolic variation nicely reflects the Taylor expansion
of eq 45 and allows
fitting of the interfacial capacitance. (left) Variation as a function
of the bulk permittivity employed in the implicit solvation model.
(right) Variation as a function of the threshold charge density (called nc) employed to define the solvation cavity.
Reproduced from ref (402). Copyright 2015 American Chemical Society.
References
-
- Gür T. M. Review of electrical energy storage technologies, materials and systems: challenges and prospects for large-scale grid storage. Energy Environ. Sci. 2018, 11, 2696–2767. 10.1039/C8EE01419A. - DOI
-
- He Q.; Yu B.; Li Z.; Zhao Y. Density functional theory for battery materials. Energy Environ. Mater. 2019, 2, 264–279. 10.1002/eem2.12056. - DOI
Publication types
LinkOut - more resources
Full Text Sources

