Serotonin neurons modulate learning rate through uncertainty
- PMID: 34936883
- PMCID: PMC8825708
- DOI: 10.1016/j.cub.2021.12.006
Serotonin neurons modulate learning rate through uncertainty
Abstract
Regulating how fast to learn is critical for flexible behavior. Learning about the consequences of actions should be slow in stable environments, but accelerate when that environment changes. Recognizing stability and detecting change are difficult in environments with noisy relationships between actions and outcomes. Under these conditions, theories propose that uncertainty can be used to modulate learning rates ("meta-learning"). We show that mice behaving in a dynamic foraging task exhibit choice behavior that varied as a function of two forms of uncertainty estimated from a meta-learning model. The activity of dorsal raphe serotonin neurons tracked both types of uncertainty in the foraging task as well as in a dynamic Pavlovian task. Reversible inhibition of serotonin neurons in the foraging task reproduced changes in learning predicted by a simulated lesion of meta-learning in the model. We thus provide a quantitative link between serotonin neuron activity, learning, and decision making.
Keywords: decision making; dorsal raphe; learning; serotonin; uncertainty.
Copyright © 2021 Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of interests The authors declare no competing interests.
Figures


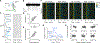
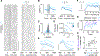



References
-
- Bertsekas DP, and Tsitsiklis JN (1996). Neuro-Dynamic Programming (Athena Scientific).
-
- Sutton RS, and Barto AG (1998). Reinforcement Learning: An Introduction (MIT Press; ).
-
- Amari S (1967). A theory of adaptive pattern classifiers. IEEE Trans. Electron. Comput EC-16, 299–307.
-
- Sutton RS (1992). Adapting bias by gradient descent: An incremental version of delta-bar-delta (AAAI), pp. 171–176.
-
- Doya K (2002). Metalearning and neuromodulation. Neural Netw. 15, 495–506. - PubMed
Publication types
MeSH terms
Substances
Associated data
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

