The Myosin Myocardial Mesh Interpreted as a Biological Analogous of Nematic Chiral Liquid Crystals

Abstract

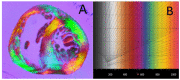
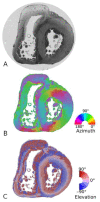
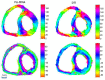
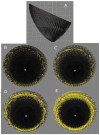
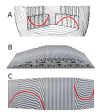
There are still grey areas in the understanding of the myoarchitecture of the ventricular mass. This is despite the progress of investigation methods since the beginning of the 21st century (diffusion tensor magnetic resonance imaging, microcomputed tomography, and polarised light imaging). The objective of this article is to highlight the specificities and the limitations of polarised light imaging (PLI) of the unstained myocardium embedded in methyl methacrylate (MMA). Thus, to better differentiate our method from other PLI modes, we will refer to it by the acronym PLI-MMA. PLI-MMA shows that the myosin mesh of the compact left ventricular wall behaves like a biological analogous of a nematic chiral liquid crystal. Results obtained by PLI-MMA are: the main direction of the myosin molecules contained in an imaged voxel, the crystal liquid director n, and a regional isotropy index RI that is an orientation tensor, the equivalent of the crystal liquid order parameter. The vector n is collinear with the first eigenvector of diffusion tensor imaging (DTI-MRI). The RI has not been confounded with the diffusion tensor of DTI that gives information about the three eigenvectors of the ellipsoid of diffusion. PLI-MMA gives no information about the collagen network. The physics of soft matter has allowed the revisiting of Streeter's conjecture on the myoarchitecture of the compact left ventricular wall: "geodesics on a nested set of toroidal surfaces". Once the torus topology is understood, this characterisation of the myoarchitecture is more accurate and parsimonious than former descriptions. Finally, this article aims to be an enthusiastic invitation to a transdisciplinary approach between physicists of liquid crystals, anatomists, and specialists of imaging.

Keywords: cardiomyocytes; liquid crystals; myoarchitecture; myosin; polarised light microscopy.

Figure 1

The myocardium embedded in the MMA behaves like a mesh of positive uniaxial crystals of myosin. (A) View of a 500 µm thick slice of a neonatal heart embedded in MMA, imaged between crossed polars with the addition of a full wave plate (path difference 540 nm). (B) Michel Levy colour chart from 0 to 1100 nm path difference. The comparison of the colours between A and B makes the visual assessment of the phase difference of the rays passing through the crystal possible.

Figure 2

The automated optical bench—the heart slice embedded in MMA is positioned on a universal stage for the acquisition of the forty-nine images necessary to extract the orientation information.

Figure 3

Example of PLI-MMA orientation maps. (A): Short-axis section of a neonatal heart, as seen in simple transmitted light after embedding in MMA resin. (B): Same section, colour-coded azimuth map with superimposition of LIC texture. (C): Colour-coded elevation map with superimposition of LIC texture. The checkered appearance (colour discontinuities at the superior and inferior part of the ventricular wall) visible on the elevation maps are due to the sudden change from 90° to −90°, when the azimuth angle ranges from 0° to 180°.

Figure 4

Comparison of the registered DTI and the downsampled PLI maps of an equatorial heart section. Upper row: azimuth maps; Lower row: elevation maps. For the sake of comparison, the representation in cartesian coordinates of PLI elevation maps was transformed in cylindrical coordinates that are the rule for DTI representation.

Figure 5

Graphical examples of tori covered with geodesics. Geodesics are pictured as close spaghetti wrapped around the torus; they wrap around the small circumference each time they wrap around the large circumference. A regular curve is right-handed when the current point moves away from the centre; the radius vector rotates counter-clockwise [28]. Column (A) Right-handed torus covered by geodesics. Column (B) Left-handed torus covered by geodesics. Top row: superior or inferior view (both are identical). Bottom row: lateral view.

Figure 6

3D model of a single torus, shaped to the compact myocardium of the left ventricle. (A) Side view of the torus regularly covered with fifty geodesics (nested tori inside are not displayed). On this torus, the external part represents the sub-endocardial region and the internal part, seen by transparency, represents the interface between the compact myocardium and the trabeculations. The torus aperture is wide in the basal part of the ventricle and becomes almost closed at the apex. (B) Three-quarter view from above of the same sketch to visualise the continuity of the geodesics from the inner and the outer part of the torus at the basal level. At this basal level, the mitral and aortic valves would reside. (C) Three-quarter view from below to visualise the continuity of the geodesics at the apical level. One can observe the geodesics invaginating at the apex from the outer surface of the torus to its inner surface. (D) Side view of an apical section. A hundred geodesics cut are coloured in orange. (E) Top view of the same section as in (D) with minimal thickness. (F) Same as in (E) with increased thickness. The segments, viewed from the top, constitute two coronas. The external corona is with a clockwise orientation and the internal one with an anticlockwise orientation. This has been described as a double spiral organisation.

Figure 7

Sketch of the Streeter model “fibres run like geodesics on a nested set of toroidal bodies of revolution” (after 16).

Figure 8

Examples of paralines and emergence of ortholines. 3D model—ten nested tori, each covered by one hundred geodesics. Theoretically, a geodesic is a curve and has no thickness, but, for the sake of representation, we gave it an arbitrary thickness or diameter as if it were spaghetti. (A) Side view of an oblique section of a set of ten nested tori, each covered by one hundred geodesics (object size 100 mm). (B–E) Slices with different thicknesses. The views are perpendicular to the section plane in A. (B) Minimal thickness slice: ortholines are resulting from the alignment of a few distinct geodesic segments. They made the measurement of an intrusion angle with the epicardial tangent plane possible. (C) Slice with same thickness as the diameter of the geodesic. This extends the length of in-plane geodesics, but the pattern becomes messy. (D) Slice with a thickness equivalent to three geodesic diameters. Emergence of paralines, i.e., the end-to-end juxtaposition of geodesic fragments running on different tori. (E) Slice thickness of five geodesic diameters.

Figure 9

(A) Parasagittal section of a set of ten nested tori, each covered by a hundred geodesics. (A’) Sagittal slice: Each orange point represents the section of one geodesic. Two ordered series of contiguous orange points draw discontinuous lines: on one are the ortholines that draw the contours of the nested tori and on the other are the paralines that connect the closest neighbouring points between different tori. Two paralines are coloured red to highlight the different orientation of their concavities on either side of the equator. (B) Near apical section of the same set of nested tori. (B’) Short axis horizontal slice. The ortholines are difficult to identify, with the exception of the two medial wall ortholines that correspond to the inner and outer wall of the deepest nested torus. The paralines describe chevron-shaped patterns, with one coloured in red (C) Oblique section: the chevron-shaped patterns vary in their orientation according to their different positions around the revolution axis of this very simplified model of the left ventricle. (C’) Reproduction of a 1943 Feneis sketch. The nested tori model explains the observed variations of the different patterns.

Figure 10

Comparison between a sketch modeled after Feneis and a sketch modeled after Bouligand. Arches highlighted in red in both diagrams illustrate the similarity of sectional artefacts seen in the ventricular myocardium and in the integuments of arthropods. (A) Feneis-like Sketch of the ventricular wall. (B) Bouligand-like sketch of the integuments of arthropods. The cuticle was cut obliquely on two sides to make a pyramid in order to reveal the plywood organisation and the progressive rotation of chitinous rods. (C) Top view of (B).