Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Nov 30;12(12):1494.
doi: 10.3390/mi12121494.

Mixing Enhancement of Non-Newtonian Shear-Thinning Fluid for a Kenics Micromixer

Abdelkader Mahammedi  1 , Naas Toufik Tayeb  2 , Kwang-Yong Kim  3 , Shakhawat Hossain  4
Affiliations

Mixing Enhancement of Non-Newtonian Shear-Thinning Fluid for a Kenics Micromixer

Abdelkader Mahammedi et al. Micromachines (Basel). .

Abstract

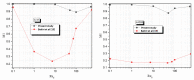
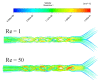
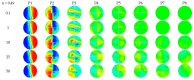
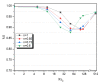
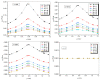
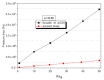
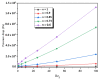
In this work, a numerical investigation was analyzed to exhibit the mixing behaviors of non-Newtonian shear-thinning fluids in Kenics micromixers. The numerical analysis was performed using the computational fluid dynamic (CFD) tool to solve 3D Navier-Stokes equations with the species transport equations. The efficiency of mixing is estimated by the calculation of the mixing index for different cases of Reynolds number. The geometry of micro Kenics collected with a series of six helical elements twisted 180° and arranged alternately to achieve the higher level of chaotic mixing, inside a pipe with a Y-inlet. Under a wide range of Reynolds numbers between 0.1 to 500 and the carboxymethyl cellulose (CMC) solutions with power-law indices among 1 to 0.49, the micro-Kenics proves high mixing Performances at low and high Reynolds number. Moreover the pressure losses of the shear-thinning fluids for different Reynolds numbers was validated and represented.

Keywords: CMC solutions; Kenics micromixer; low Reynolds number; mixing index; non-Newtonian fluids; numerical simulation.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Kenics micromixer.
Figure 2
Figure 2
Evolution of mixing index (MI) with Reynolds number for a Newtonian fluid compared with Houssain et al. [20].
Figure 3
Figure 3
Evolution of mixing index of Reynolds number for a Newtonian and non-Newtonian fluid compared with Bahiri et al. [15].
Figure 3
Figure 3
Evolution of mixing index of Reynolds number for a Newtonian and non-Newtonian fluid compared with Bahiri et al. [15].
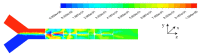
Figure 4
Figure 4
Distribution of mass fraction at Reg = 25, n = 0.73.
Figure 5
Figure 5
Velocity streamlines of n = 0.73 with different Reynolds number.
Figure 6
Figure 6
Contour of mass fraction at cross-section P1–P8 for different Reynolds numbers with n = 1.
Figure 7
Figure 7
Contours of mass fraction at cross-section P1–P8 for different Reynolds numbers with n = 0.49.
Figure 8
Figure 8
Development of mixing index versus generalized Reynolds number for differences values of power-law index.
Figure 9
Figure 9
Development of mixing index along the mixing helical for different power-law indices and Reynolds numbers.
Figure 9
Figure 9
Development of mixing index along the mixing helical for different power-law indices and Reynolds numbers.
Figure 10
Figure 10
Shear rate profiles and apparent viscosity profiles on line x = 0 at the exit plane for different power-law indices.
Figure 11
Figure 11
Apparent viscosity profiles on line x = 0 at the exit plane for different Reynolds numbers and different power-law indices.
Figure 12
Figure 12
Pressure drop vs. Reynolds numbers compared with TLCC micromixer for n = 0.73.
Figure 13
Figure 13
Variations of the pressure drop with generalized Reynolds number for different power-law indices.
See this image and copyright information in PMC

References

    1. Jeong G.S., Chung S., Kim C.B., Lee S.H. Applications of Micromixing Technology. Analyst. 2010;135:460–473. doi: 10.1039/b921430e. - DOI - PubMed
    1. Minye L. Computational study of convective—Diffusive mixing in a microchannel mixer. Chem. Eng. Sci. 2011;66:2211–2223.
    1. Nguyen N.T., Wu Z. Micromixers—A review. J. Micromech. Microeng. 2005;15:1. doi: 10.1088/0960-1317/15/2/R01. - DOI
    1. Hessel V., Lowe H., Schönfeld F. Micromixers—A review on passive and active mixing principles. Chem. Eng. Sci. 2005;60:2479–2501. doi: 10.1016/j.ces.2004.11.033. - DOI
    1. Okuducu M.B., Aral M.M. Performance Analysis and Numerical Evaluation of Mixing in 3-D T-Shape Passive Micromixers. Micromachines. 2018;9:210. doi: 10.3390/mi9050210. - DOI - PMC - PubMed

LinkOut - more resources