Nonlinear Hyperparameter Optimization of a Neural Network in Image Processing for Micromachines

Abstract

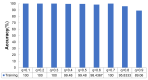
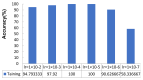
Deep neural networks are widely used in the field of image processing for micromachines, such as in 3D shape detection in microelectronic high-speed dispensing and object detection in microrobots. It is already known that hyperparameters and their interactions impact neural network model performance. Taking advantage of the mathematical correlations between hyperparameters and the corresponding deep learning model to adjust hyperparameters intelligently is the key to obtaining an optimal solution from a deep neural network model. Leveraging these correlations is also significant for unlocking the "black box" of deep learning by revealing the mechanism of its mathematical principle. However, there is no complete system for studying the combination of mathematical derivation and experimental verification methods to quantify the impacts of hyperparameters on the performances of deep learning models. Therefore, in this paper, the authors analyzed the mathematical relationships among four hyperparameters: the learning rate, batch size, dropout rate, and convolution kernel size. A generalized multiparameter mathematical correlation model was also established, which showed that the interaction between these hyperparameters played an important role in the neural network's performance. Different experiments were verified by running convolutional neural network algorithms to validate the proposal on the MNIST dataset. Notably, this research can help establish a universal multiparameter mathematical correlation model to guide the deep learning parameter adjustment process.

Keywords: deep neural network; hyperparameters; image processing; multiparameter mathematical correlation model.

Figure 1

Training accuracies obtained under different q (%).

Figure 2

Model convergence under different q: (a) convergence of training cross-entropy loss; (b) convergence of test accuracy.

Figure 3

Training accuracies obtained under different m (%).

Figure 4

Model convergence under different m: (a) convergence of training cross-entropy loss; (b) convergence of test accuracy.

Figure 5

Training accuracies obtained under different lr (%).

Figure 6

Model convergence with different lr: (a) convergence of training cross-entropy loss; (b) convergence of testing accuracy.

Figure 7

Training accuracies obtained under different ke (%).

Figure 8

Model convergence with ke: (a) convergence of training cross-entropy loss; (b) convergence of test accuracy.

Figure 9

Training accuracies and test accuracies obtained for the confirmatory experiment (%).

Figure 10

Model convergence for the confirmatory experiment: (a) convergence of training cross-entropy loss; (b) convergence of test accuracy.

Figure 11

Statistical box plots of LRelu, Relu, and Selu models under different steps for 10 times experiment results: (a) testing accuracy of LRelu; (b) training loss of LRelu; (c) testing accuracy of Relu; (d) training loss of Relu; (e) testing accuracy of Selu; (f) training loss of Selu.