Asynchronous and Coherent Dynamics in Balanced Excitatory-Inhibitory Spiking Networks
- PMID: 34955768
- PMCID: PMC8702645
- DOI: 10.3389/fnsys.2021.752261
Asynchronous and Coherent Dynamics in Balanced Excitatory-Inhibitory Spiking Networks
Abstract
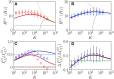
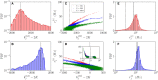
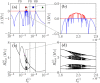
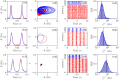
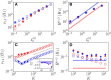
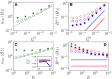
Dynamic excitatory-inhibitory (E-I) balance is a paradigmatic mechanism invoked to explain the irregular low firing activity observed in the cortex. However, we will show that the E-I balance can be at the origin of other regimes observable in the brain. The analysis is performed by combining extensive simulations of sparse E-I networks composed of N spiking neurons with analytical investigations of low dimensional neural mass models. The bifurcation diagrams, derived for the neural mass model, allow us to classify the possible asynchronous and coherent behaviors emerging in balanced E-I networks with structural heterogeneity for any finite in-degree K. Analytic mean-field (MF) results show that both supra and sub-threshold balanced asynchronous regimes are observable in our system in the limit N >> K >> 1. Due to the heterogeneity, the asynchronous states are characterized at the microscopic level by the splitting of the neurons in to three groups: silent, fluctuation, and mean driven. These features are consistent with experimental observations reported for heterogeneous neural circuits. The coherent rhythms observed in our system can range from periodic and quasi-periodic collective oscillations (COs) to coherent chaos. These rhythms are characterized by regular or irregular temporal fluctuations joined to spatial coherence somehow similar to coherent fluctuations observed in the cortex over multiple spatial scales. The COs can emerge due to two different mechanisms. A first mechanism analogous to the pyramidal-interneuron gamma (PING), usually invoked for the emergence of γ-oscillations. The second mechanism is intimately related to the presence of current fluctuations, which sustain COs characterized by an essentially simultaneous bursting of the two populations. We observe period-doubling cascades involving the PING-like COs finally leading to the appearance of coherent chaos. Fluctuation driven COs are usually observable in our system as quasi-periodic collective motions characterized by two incommensurate frequencies. However, for sufficiently strong current fluctuations these collective rhythms can lock. This represents a novel mechanism of frequency locking in neural populations promoted by intrinsic fluctuations. COs are observable for any finite in-degree K, however, their existence in the limit N >> K >> 1 appears as uncertain.
Keywords: asynchronous dynamics; balanced spiking neural populations; coherent chaos; collective oscillations; neural mass model; quadratic integrate and fire neuron; sparse inhibitory-excitatory networks; structural heterogeneity.
Copyright © 2021 Bi, di Volo and Torcini.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures

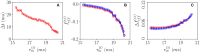
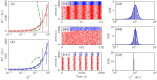
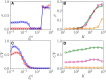
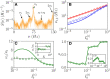
References
-
- Angulo-Garcia D., Luccioli S., Olmi S., Torcini A. (2017). Death and rebirth of neural activity in sparse inhibitory networks. New J. Phys. 19:053011. 10.1088/1367-2630/aa69ff - DOI
-
- Benettin G., Galgani L., Giorgilli A., Strelcyn J.-M. (1980). Lyapunov characteristic exponents for smooth dynamical systems and for hamiltonian systems; a method for computing all of them. part 1: Theory. Meccanica 15, 9–20. 10.1007/BF02128236 - DOI
LinkOut - more resources
Full Text Sources

