Numerical Study of the Effect of Thixotropy on Extrudate Swell

Abstract

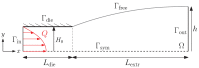
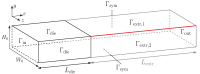
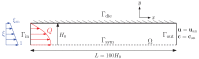
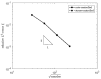
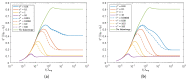
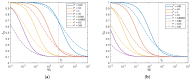
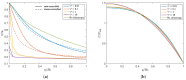
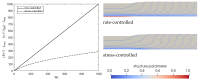
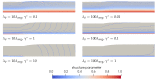
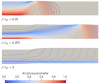
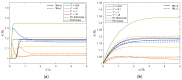
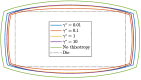
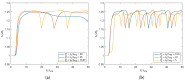
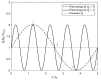
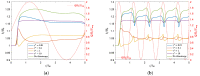
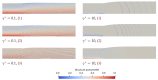
The extrusion of highly filled elastomers is widely used in the automotive industry. In this paper, we numerically study the effect of thixotropy on 2D planar extrudate swell for constant and fluctuating flow rates, as well as the effect of thixotropy on the swell behavior of a 3D rectangular extrudate for a constant flowrate. To this end, we used the Finite Element Method. The state of the network structure in the material is described using a kinetic equation for a structure parameter. Rate and stress-controlled models for this kinetic equation are compared. The effect of thixotropy on extrudate swell is studied by varying the damage and recovery parameters in these models. It was found that thixotropy in general decreases extrudate swell. The stress-controlled approach always predicts a larger swell ratio compared to the rate-controlled approach for the Weissenberg numbers studied in this work. When the damage parameter in the models is increased, a less viscous fluid layer appears near the die wall, which decreases the swell ratio to a value lower than the Newtonian swell ratio. Upon further increasing the damage parameter, the high viscosity core layer becomes very small, leading to an increase in the swell ratio compared to smaller damage parameters, approaching the Newtonian value. The existence of a low-viscosity outer layer and a high-viscosity core in the die have a pronounced effect on the swell ratio for thixotropic fluids.

Keywords: FEM; extrudate swell; thixotropy; viscoelasticity.

Figure 1

Schematic representation of the 2D planar extrudate swell problem. The free surface of the extrudate is indicated in gray.

Figure 2

Schematic representation of the 3D problem of an extrudate emerging from a rectangular die. The corner line used in the corner-line method is depicted in red.

Figure 3

Schematic representation of the 2D channel problem used in the convergence study.

Figure 4

Relative error in $$\xi$$ at the outlet of the channel for 2D meshes with different element sizes.

Figure 5

Two-dimensional planar swell mesh one uniform refinement step coarser compared to the mesh used throughout the remainder of this paper.

Figure 6

Three-dimensional mesh used in this study. Refinement factor at the die exit is 5.

Figure 7

Relative error in $$\xi$$ at the outlet of the channel at time $$t={\lambda }_0$$, for different time step sizes $$\mathsf{\Delta }t$$ for the rate and stress-controlled approach.

Figure 8

Transient polymer viscosity for $${\dot{\gamma }}_{\mathrm{c}}$$, where $${\gamma }^{*}$$ and $${\tau }^{*}$$ are chosen such that $${\xi }_{\mathrm{eq}}$$ is matched for the rate and stress-controlled approach to obtain the same steady-state rheology for both models. (a) $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$. (b) $${\lambda }_{\theta }=100{\lambda }_{\mathrm{avg}}$$.

Figure 9

Equilibrium structure parameter $${\xi }_{\mathrm{eq}}$$ as a function of Weissenberg number. Here, $${\gamma }^{*}$$ and $${\tau }^{*}$$ are chosen such that $${\xi }_{\mathrm{eq}}$$ is matched for the rate and stress-controlled approach at a characteristic shear rate $${\dot{\gamma }}_{\mathrm{c}}$$. (a) $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$. (b) $${\lambda }_{\theta }=100{\lambda }_{\mathrm{avg}}$$.

Figure 10

Swell ratio as a function of dimensionless time of the point of the free surface on $${\mathsf{\Gamma }}_{\mathrm{out}}$$ for different values of $${\gamma }^{*}$$ for the rate-controlled approach and the corresponding value of $${\tau }^{*}$$ for the stress-controlled approach. (a) $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$ and (b) $${\lambda }_{\theta }=100{\lambda }_{\mathrm{avg}}$$. Solid lines are the rate-controlled model predictions, dashed lines are the corresponding stress-controlled model predictions. The black dashed line indicates the Newtonian swell ratio. (a) $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$. (b) $${\lambda }_{\theta }=100{\lambda }_{\mathrm{avg}}$$.

Figure 11

Total shear viscosity divided by the zero-shear viscosity predicted by the rate-controlled approach for $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$ and different damage parameters $${\gamma }^{*}$$.

Figure 12

Ratio of the total viscosity and the zero-shear viscosity over the die height at $${\mathsf{\Gamma }}_{\mathrm{in}}$$ for $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$ and different damage parameters for the rate and stress-controlled approaches (a). Dimensionless velocity magnitude over the die height at $${\mathsf{\Gamma }}_{\mathrm{in}}$$ for $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$ and different damage parameters for the rate-controlled approach (b). (a) $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$. (b) $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$.

Figure 13

Damage terms of the rate and stress-controlled approaches as a function of Weissenberg number in steady shear (left). Contour plots of the structure parameter $$\xi$$ for $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$ an $${\gamma }^{*}=1$$ for the rate-controlled approach and the corresponding values for the stress controlled approach (right). Unless indicated otherwise, all contour plots presented in this paper are made with equidistant contour lines with an interval of 0.01.

Figure 14

Contour plots of the structure parameter $$\xi$$ predicted by the rate-controlled approach for $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$ (left) and $${\lambda }_{\theta }=100{\lambda }_{\mathrm{avg}}$$ (right) for different damage parameter and recovery time scale combinations that give the same $${\xi }_{\mathrm{eq}}$$.

Figure 15

Contour plots of the structure parameter $$\xi$$ predicted by the rate-controlled approach for $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$ and $${\gamma }^{*}=1$$ for different instances in time.

Figure 16

Swell ratio as a function of dimensionless time for the point of the free surface on $${\mathsf{\Gamma }}_{\mathrm{out}}$$ (a) and final swell ratio of the free surface as a function of the x-coordinate along the free surface (b). Here, $$x/H_0=0$$ corresponds to the x-coordinate at the die exit. Results are obtained for different values of $${\gamma }^{*}$$ for the rate-controlled approach using two different Weissenberg numbers. Solid lines indicate the results for $$\mathrm{Wi}=5$$, whereas dashed lines indicate the results for $$\mathrm{Wi}=1$$.

Figure 17

Contour of a 3D extrudate of a thixotropic viscoelastic fluid. Evolution of the structure in the material is modeled using the rate-controlled approach with $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$ and different damage parameters for $$\mathrm{Wi}=5$$.

Figure 18

Swell ratio as a function of dimensionless time for the point of the free surface on $${\mathsf{\Gamma }}_{\mathrm{out}}$$, for a sinusoidal flow rate with dimensionless frequency $$f^{*}=1/t_{\mathrm{p}}^{*}$$, with $$t_{\mathrm{p}}^{*}=t_{\mathrm{p}}/{\lambda }_{\mathrm{avg}}$$.

Figure 19

Sinusoidal flow rate with dimensionless period $$t_{\mathrm{p}}^{*}=t_{\mathrm{p}}/{\lambda }_{\theta }=1$$ (solid line), and $$t_{\mathrm{p}}^{*}=t_{\mathrm{p}}/{\lambda }_{\theta }=5$$ (dashed line) and the constant flow rate applied in previous results (dotted line).

Figure 20

Swell ratio as a function of dimensionless time for the point of the free surface on $${\mathsf{\Gamma }}_{\mathrm{out}}$$, for different values of $${\gamma }^{*}$$ and a sinusoidal flow rate with dimensionless frequency $$f^{*}=1/t_{\mathrm{p}}^{*}$$, with $$t_{\mathrm{p}}^{*}=t_{\mathrm{p}}/{\lambda }_{\theta }=5$$ (a), and $$t_{\mathrm{p}}^{*}=t_{\mathrm{p}}/{\lambda }_{\theta }=1$$ (b). The red dotted line represents the applied flow rate.

Figure 21

Contour plots of the structure parameter $$\xi$$ predicted by the rate-controlled approach for $${\lambda }_{\theta }=10{\lambda }_{\mathrm{avg}}$$ and $${\gamma }^{*}=0.1$$ (left) and $${\gamma }^{*}=10$$ (right) for different instances in time as indicated by the red numbers in Figure 19 for a fluctuating flowrate Q. The contour plots in this figure are made with equidistant contour lines with an interval of 0.025 for clarity.