Non-Isothermal Free-Surface Viscous Flow of Polymer Melts in Pipe Extrusion Using an Open-Source Interface Tracking Finite Volume Method

Abstract

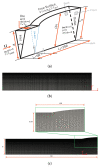
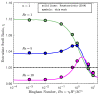
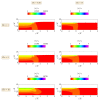
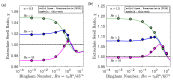
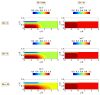
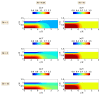
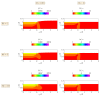
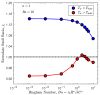
Polymer extrudate swelling is a rheological phenomenon that occurs after polymer melt flow emerges at the die exit of extrusion equipment due to molecular stress relaxations and flow redistributions. Specifically, with the growing demand for large scale and high productivity, polymer pipes have recently been produced by extrusion. This study reports the development of a new incompressible non-isothermal finite volume method, based on the Arbitrary Lagrangian-Eulerian (ALE) formulation, to compute the viscous flow of polymer melts obeying the Herschel-Bulkley constitutive equation. The Papanastasiou-regularized version of the constitutive equation is employed. The influence of the temperature on the rheological behavior of the material is controlled by the Williams-Landel-Ferry (WLF) function. The new method is validated by comparing the extrudate swell ratio obtained for Bingham and Herschel-Bulkley flows (shear-thinning and shear-thickening) with reference data found in the scientific literature. Additionally, the essential flow characteristics including yield-stress, inertia and non-isothermal effects were investigated.

Keywords: Herschel–Bulkley fluids; OpenFOAM; extrudate swell; finite volume method; free-surfaces; interface tracking; pipe die; polymer melt; yield stress.

Figure 1

Schematic representation of (a) the axisymmetric extrudate swell domain geometry and boundary faces (b) of an indicative discretization mesh at the initial time step $$t=0$$, and (c) at steady state.

Figure 2

Steady-state extrudate swell ratio $$\chi$$ for the isothermal extrudate swell of Bingham fluids ($$n=1$$) at $$Re=\{1,5,10\}$$ and $$Bn=\{{10}^{-3},{10}^{-2},{10}^{-1},0.5,1,5,10\}$$. Solid lines represent the results obtained by Kountouriotis et al. [41], and the symbols represent the results obtained by the newly developed interface tracking code.

Figure 3

Contours of the magnitude of the polymer velocity vector at steady-state for the isothermal extrudate swell of Bingham fluids ($$n=1$$) when $$Re=1$$ (top), $$Re=5$$ (middle) and $$Re=10$$ (bottom), and $$Bn=0.001$$ (left) and $$Bn=10$$ (right).

Figure 4

Contours of the magnitude of the polymer stress tensor at steady-state for the isothermal extrudate swell of Bingham fluids ($$n=1$$) when $$Re=1$$ (top), $$Re=5$$ (middle) and $$Re=10$$ (bottom), and $$Bn=0.001$$ (left) and $$Bn=10$$ (right).

Figure 5

Steady-state extrudate swell ratio $$\chi$$ for the isothermal extrudate swell of Herschel–Bulkley fluids at $$Re=\{1,5,10\}$$ and $$Bn=\{{10}^{-3},{10}^{-2},{10}^{-1},0.5,1,5,10\}$$ with (a) $$n=0.5$$ and (b) $$n=1.5$$. Solid lines represent the results obtained by Kountouriotis et al. [41], and the symbols represent the results obtained by the newly developed interface tracking code.

Figure 6

Contours of the magnitude of the polymer velocity vector at steady-state for the isothermal extrudate swell of shear-thinning Herschel–Bulkley fluids ($$n=0.5$$) when $$Re=1$$ (top), $$Re=5$$ (middle) and $$Re=10$$ (bottom), and $$Bn=0.001$$ (left) and $$Bn=10$$ (right).

Figure 7

Contours of the magnitude of the polymer stress tensor at steady state for the isothermal extrudate swell of shear-thinning Herschel–Bulkley fluids ($$n=0.5$$) when $$Re=1$$ (top), $$Re=5$$ (middle) and $$Re=10$$ (bottom), and $$Bn=0.001$$ (left) and $$Bn=10$$ (right).

Figure 8

Contours of the magnitude of the polymer velocity vector at steady state for the isothermal extrudate swell of shear-thickening Herschel–Bulkley fluids ($$n=1.5$$) when $$Re=1$$ (top), $$Re=5$$ (middle) and $$Re=10$$ (bottom), and $$Bn=0.001$$ (left) and $$Bn=10$$ (right).

Figure 9

Contours of the magnitude of the polymer stress tensor at steady-state for the isothermal extrudate swell of shear-thickening Herschel–Bulkley fluids ($$n=1.5$$) when $$Re=1$$ (top), $$Re=5$$ (middle) and $$Re=10$$ (bottom), and $$Bn=0.001$$ (left) and $$Bn=10$$ (right).

Figure 10

Steady-state extrudate swell ratio $$\chi$$ for the non-isothermal axisymmetric extrudate swell of Bingham fluids ($$n=1$$) at $$Re=10$$ and $$Bn=\{{10}^{-3},{10}^{-2},{10}^{-1},0.5,1,2,3,4,5,10\}$$.

Figure 11

Contours of the magnitude of the polymer velocity vector at steady-state for the non-isothermal asymmetric extrudate swell flow of Bingham fluids ($$n=1$$) at $$Re=10$$ for $$Bn=0.001$$ (left) and $$Bn=10$$ (right), when $$T_w<T_{inlet}$$ (top) and $$T_w>T_{inlet}$$ (bottom).

Figure 12

Contours of dimensionless temperature at steady-state for the non-isothermal asymmetric extrudate swell flow of Bingham fluids ($$n=1$$) at $$Re=10$$ for $$Bn=0.001$$ (left) and $$Bn=10$$ (right), when $$T_w<T_{inlet}$$ (top) and $$T_w>T_{inlet}$$ (bottom).