An algorithm for the direct estimation of the parameters of the SIR epidemic model from the I(t) dynamics

Abstract

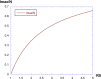
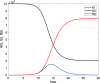
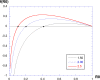
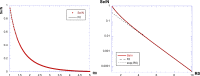
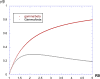
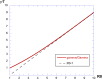
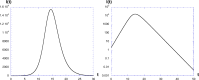
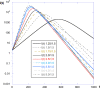
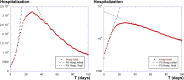
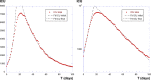
The discrete SIR (Susceptible-Infected-Recovered) model is used in many studies to model the evolution of epidemics. Here, we consider one of its dynamics-the exponential decrease in infected cases I(t). By considering only the I(t) dynamics, we extract three parameters: the exponent of the initial exponential increase $\gamma$ ; the maximum value $I_{max}$ ; and the exponent of the final decrease $\Gamma$ . From these three parameters, we show mathematically how to extract all relevant parameters of the SIR model. We test this procedure on numerical data and then apply the methodology to real data received from the COVID-19 situation in France. We conclude that, based on the hospitalized data and the ICU (Intensive Care Unit) cases, two exponentials are found, for the initial increase and the decrease in I(t). The parameters found are larger than reported in the literature, and they are associated with a susceptible population which is limited to a sub-sample of the total population. This may be due to the fact that the SIR model cannot be applied to the covid-19 case, due to its strong hypotheses such as mixing of all the population, or also to the fact that the parameters have changed over time, due to the political initiatives such as social distanciation and lockdown.

Fig. 1

Maximum value of $\frac{I_{max}}{N}$ given by Eq. (10)

Fig. 2

An example of dynamics of S(t), R(t) and S(t), chosen for the parameters $I_0=2$, $N=100,000$, $\beta =1.5$ and $R_0=2$. This illustrates the fact that $I(t)\to 0$ and $S(t)\to S_e$, as $t\to \infty$

Fig. 3

Solving the equation $f(x)=\frac{1}{R_0}log(x)+1-x=0$ for each value of $R_0$: here, three examples with $R_0=1.5$, 2 and 2.5. The intersection of the horizontal axis gives the value of $S_e/N$

Fig. 4

Solving the equation $log(x)/R_0+1-x=0$ for each value of $R_0$ we have the curve $S_e(R_0)$. Left: linear plot; right: log-linear plot to emphasize the asymptotic exponential curve

Fig. 5

Plot of $\gamma /\beta$ and $\Gamma /\beta$ versus $R_0$. The first exponent is increasing monotonically, whereas the second one reaches a maximum value of 0.2984 for $R_0\simeq 2.15$, after which it decreases. We also see that we have always $\gamma >\Gamma$

Fig. 6

Plot of the ratio $\rho =\gamma /\Gamma$: we see an almost linear increase, for values of $R_0$ larger than 6, with an asymptotic value of $R_0-1$ as expected. When the two exponents are known and estimated, this ratio can be used to extract directly the value or $R_0$

Fig. 7

Plot of I(t) for $I_0=2$, $N=100,000$, $R_0=2.0$ and $\beta =1.5$. Right: a log-linear plot showing the exponential increase and decrease

Fig. 8

Plot of I(t) for $\beta =1.5$ and different values of $R_0$. We see that all curves have similar behavior, with different time values for the maximum, and also different decrease and increase slopes

Fig. 9

Plot of $I_H(t)$ of the total hospitalized people in France due to COVID-19. Left panel: linear coordinates with exponential fits; right panel: log-linear plot with the two fits as straight lines

Fig. 10

Plot of $I_{\mathit{icu}}(t)$ of people in intensive care unit in France due to COVID-19. Left panel: linear coordinates; right panel: log-linear plot. The log-linear plot shows two exponential behavior