Modeling Early Phases of COVID-19 Pandemic in Northern Italy and Its Implication for Outbreak Diffusion
- PMID: 34976909
- PMCID: PMC8716563
- DOI: 10.3389/fpubh.2021.724362
Modeling Early Phases of COVID-19 Pandemic in Northern Italy and Its Implication for Outbreak Diffusion
Abstract
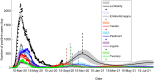
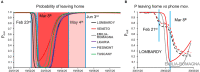
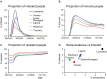
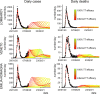
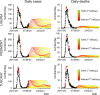
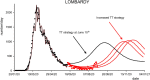
The COVID-19 pandemic has sparked an intense debate about the hidden factors underlying the dynamics of the outbreak. Several computational models have been proposed to inform effective social and healthcare strategies. Crucially, the predictive validity of these models often depends upon incorporating behavioral and social responses to infection. Among these tools, the analytic framework known as "dynamic causal modeling" (DCM) has been applied to the COVID-19 pandemic, shedding new light on the factors underlying the dynamics of the outbreak. We have applied DCM to data from northern Italian regions, the first areas in Europe to contend with the outbreak, and analyzed the predictive validity of the model and also its suitability in highlighting the hidden factors governing the pandemic diffusion. By taking into account data from the beginning of the pandemic, the model could faithfully predict the dynamics of outbreak diffusion varying from region to region. The DCM appears to be a reliable tool to investigate the mechanisms governing the spread of the SARS-CoV-2 to identify the containment and control strategies that could efficiently be used to counteract further waves of infection.
Keywords: COVID-19; DCM—dynamic causal modeling; brain modeling; computational modeling; predictive modeling.
Copyright © 2021 Gandolfi, Pagnoni, Filippini, Goffi, Vinceti, D'Angelo and Mapelli.
Conflict of interest statement
AG is employed by TerrAria s.r.l. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures
Similar articles
-
Covid-19 Outbreak Progression in Italian Regions: Approaching the Peak by the End of March in Northern Italy and First Week of April in Southern Italy.Int J Environ Res Public Health. 2020 Apr 27;17(9):3025. doi: 10.3390/ijerph17093025. Int J Environ Res Public Health. 2020. PMID: 32349259 Free PMC article.
-
Inappropriate risk perception for SARS-CoV-2 infection among Italian HCWs in the eve of COVID-19 pandemic.Acta Biomed. 2020 May 14;91(3):e2020040. doi: 10.23750/abm.v91i3.9727. Acta Biomed. 2020. PMID: 32921735 Free PMC article.
-
Monitoring emergency calls and social networks for COVID-19 surveillance. To learn for the future: The outbreak experience of the Lombardia region in Italy.Acta Biomed. 2020 Jul 20;91(9-S):29-33. doi: 10.23750/abm.v91i9-S.10038. Acta Biomed. 2020. PMID: 32701914 Free PMC article.
-
COVID-19: update of the Italian situation.J Neurovirol. 2020 Dec;26(6):834-837. doi: 10.1007/s13365-020-00900-w. Epub 2020 Sep 8. J Neurovirol. 2020. PMID: 32901393 Free PMC article. Review.
-
COVID-19 on the Nile: Review on the Management and Outcomes of the COVID-19 Pandemic in the Arab Republic of Egypt from February to August 2020.Int J Environ Res Public Health. 2021 Feb 8;18(4):1588. doi: 10.3390/ijerph18041588. Int J Environ Res Public Health. 2021. PMID: 33567519 Free PMC article. Review.
Cited by
-
A 12-month projection to September 2022 of the COVID-19 epidemic in the UK using a dynamic causal model.Front Public Health. 2022 Nov 15;10:999210. doi: 10.3389/fpubh.2022.999210. eCollection 2022. Front Public Health. 2022. PMID: 36457320 Free PMC article.
-
Dynamic causal models in infectious disease epidemiology-an assessment of their predictive validity based on the COVID-19 epidemic in the UK 2020 to 2024.Front Public Health. 2025 May 2;13:1573783. doi: 10.3389/fpubh.2025.1573783. eCollection 2025. Front Public Health. 2025. PMID: 40385629 Free PMC article.
-
Inferring Trajectories of Psychotic Disorders Using Dynamic Causal Modeling.Comput Psychiatr. 2023 Aug 28;7(1):60-75. doi: 10.5334/cpsy.94. eCollection 2023. Comput Psychiatr. 2023. PMID: 38774642 Free PMC article.
References
-
- Kucharski AJ, Klepac P, Conlan AJK, Kissler SM, Tang ML, Fry H, et al. . Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: a mathematical modelling study. Lancet Infect Dis. (2020) 20:1151. 10.1016/S1473-3099(20)30457-6 - DOI - PMC - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
Miscellaneous

