The many facets of shape
- PMID: 34982105
- PMCID: PMC8742511
- DOI: 10.1167/jov.22.1.1
The many facets of shape
Abstract
Shape is an interesting property of objects because it is used in ordinary discourse in ways that seem to have little connection to how it is typically defined in mathematics. The present article describes how the concept of shape can be grounded within Euclidean and non-Euclidean geometry and also to human perception. It considers the formal methods that have been proposed for measuring the differences among shapes and how the performance of those methods compares with shape difference thresholds of human observers. It discusses how different types of shape change can be perceptually categorized. It also evaluates the specific data structures that have been used to represent shape in models of both human and machine vision, and it reviews the psychophysical evidence about the extent to which those models are consistent with human perception. Based on this review of the literature, we argue that shape is not one thing but rather a collection of many object attributes, some of which are more perceptually salient than others. Because the relative importance of these attributes can be context dependent, there is no obvious single definition of shape that is universally applicable in all situations.
Figures







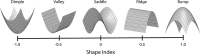
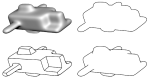
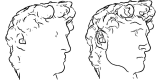
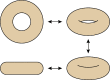


Similar articles
-
Vernier judgments in the absence of regular shape information.Vision Res. 1999 Jul;39(14):2349-60. doi: 10.1016/s0042-6989(98)00265-x. Vision Res. 1999. PMID: 10367056
-
Determining the similarity of deformable shapes.Vision Res. 1998 Aug;38(15-16):2365-85. doi: 10.1016/s0042-6989(98)00043-1. Vision Res. 1998. PMID: 9798005
-
Perceived orientation of complex shape reflects graded part decomposition.J Vis. 2006 Jul 14;6(8):805-21. doi: 10.1167/6.8.4. J Vis. 2006. PMID: 16895460
-
[Principles and methods of geometric morphometrics].Zh Obshch Biol. 2002 Nov-Dec;63(6):473-93. Zh Obshch Biol. 2002. PMID: 12510587 Review. Russian.
-
Probing intermediate stages of shape processing.J Vis. 2015;15(7):1. doi: 10.1167/15.7.1. J Vis. 2015. PMID: 26024510 Review.
Cited by
-
Are mirror-symmetric objects of special importance for 3D shape perception? A reply to Sawada and Pizlo (2022).J Vis. 2022 Mar 2;22(4):16. doi: 10.1167/jov.22.4.16. J Vis. 2022. PMID: 35344020 Free PMC article.
-
Using compositionality to understand parts in whole objects.Eur J Neurosci. 2022 Aug;56(4):4378-4392. doi: 10.1111/ejn.15746. Epub 2022 Jul 20. Eur J Neurosci. 2022. PMID: 35760552 Free PMC article. Review.
-
Homology judgements of pre-evolutionary naturalists explained by general human shape matching abilities.Sci Rep. 2023 Jul 28;13(1):12269. doi: 10.1038/s41598-023-39036-2. Sci Rep. 2023. PMID: 37507447 Free PMC article.
-
Competition Between Object Topology and Surface Features in Children's Extension of Novel Nouns.Open Mind (Camb). 2023 Apr 5;7:93-110. doi: 10.1162/opmi_a_00073. eCollection 2023. Open Mind (Camb). 2023. PMID: 37416072 Free PMC article.
References
-
- Alcorn, M. A., Li, Q., Gong, Z., Wang, C., Mai, L., Ku, W., & Nguyen, A. (2019). Strike (with) a pose: Neural networks are easily fooled by strange poses of familiar objects. In CVPR, Computer Vision Foundation/IEEE (pp. 4845–4854).
-
- Anderson, M., & Feil, T. (2015). A first course in abstract algebra (3rd ed.). Boca Raton, FL: CRC Press.
-
- Attneave, F. (1954). Some informational aspects of visual perception. Psychological Review, 61, 183–193. - PubMed
-
- Belhumeur, P., Kriegman, D. J., & Yuille, A. L. (1997). The bas relief ambiguity. In Proceedings of the 1997 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (pp. 1060–1066). Washington, DC: IEEE Computer Society Press.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

