Learning Cortical Parcellations Using Graph Neural Networks

Abstract

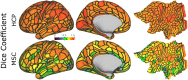
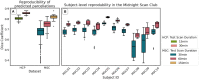
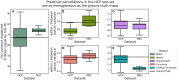
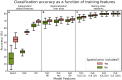
Deep learning has been applied to magnetic resonance imaging (MRI) for a variety of purposes, ranging from the acceleration of image acquisition and image denoising to tissue segmentation and disease diagnosis. Convolutional neural networks have been particularly useful for analyzing MRI data due to the regularly sampled spatial and temporal nature of the data. However, advances in the field of brain imaging have led to network- and surface-based analyses that are often better represented in the graph domain. In this analysis, we propose a general purpose cortical segmentation method that, given resting-state connectivity features readily computed during conventional MRI pre-processing and a set of corresponding training labels, can generate cortical parcellations for new MRI data. We applied recent advances in the field of graph neural networks to the problem of cortical surface segmentation, using resting-state connectivity to learn discrete maps of the human neocortex. We found that graph neural networks accurately learn low-dimensional representations of functional brain connectivity that can be naturally extended to map the cortices of new datasets. After optimizing over algorithm type, network architecture, and training features, our approach yielded mean classification accuracies of 79.91% relative to a previously published parcellation. We describe how some hyperparameter choices including training and testing data duration, network architecture, and algorithm choice affect model performance.

Keywords: brain; functional connectivity; graph neural network; human; parcellation; representation learning; segmentation.

Figure 1

Each layer, l, implicitly aggregates more distant neighborhood signals into a node update. The first layer aggregates information over immediately adjacent neighbors, while the second, third, etc. layers incorporate signals from increasingly larger neighborhoods.

Figure 2

Graph attention network employing a jumping-knowledge mechanism. The network takes as input the graph adjacency structure and the nodewise feature matrix, and outputs a node-by-label logit matrix. Each GATConv block is composed of multiple attention heads. Arrows indicate the direction of processing. Aggregation function, g(x), which takes as input the embeddings from each GATConv block, learns a convex combination of the layer-wise embeddings.

Figure 3

Subject-level (A) and group-level (B) predictions generated by the optimal model in the MSC (left) and HCP (middle) datasets.

Figure 4

Average accuracy maps for the HCP test set using the optimal model, computed by averaging the classification error maps across all HCP dataset test subjects. (A) Blue (0.0) = vertex incorrectly classified in all test subjects; Red (1.0) = vertex correctly classified in all test subjects. Areas in the lateral prefrontal and ventral/dorsal occipital areas showed the highest error rates. (B) Errors occur most frequently at the boundaries of cortical regions. Black lines represent areal boundaries of the consensus prediction parcellation.

Figure 5

Mean model probabilities for a subset of cortical areas for the HCP (top) and MSC (middle) datasets computed using the optimal model, and the MMP binary class probabilities from Glasser et al. (2016) and Coalson et al. (2018) (bottom). Probabilistic maps are illustrated for areas V1, 46, TE1a, LIPv, MT, RSC, and 10r. These maps are thresholded at a minimum probability value of 0.005, the probability of randomly assigning a vertex to one of the 180 cortical areas.

Figure 6

Mean areal Dice coefficient estimates, computed using the optimal model on 15-min HCP data (4 repeated sessions) and 30-min MSC data (10 repeated sessions), normalized with the same color map. Estimates are computed for each area, and averaged across all subjects.

Figure 7

Reproducibility of predicted maps generated by the optimal model, as measured using the Dice coefficient. We show mean reproducibility estimates for each dataset (A), and subject-level estimates in the Midnight Scan Club (B). Estimates for 60 min (HCP) and 300 min (MSC) durations are not shown in (A) because there is only one image per subject for these durations. Similarly, estimates for 150 min durations are not shown in (B) because there is only a single scalar estimate per subject.

Figure 8

Homogeneity of predicted parcellations in the HCP and MSC datasets using the optimal model. (A) Predicted parcels in the HCP test set explained as much variability in the functional connectivity as the ground truth parcels. (B–E) Predictions in the MSC had more variable myelin content and less variable cortical thickness estimates, relative to the HCP predictions.

Figure 9

Classification accuracy as a function of model features, using the optimal model architecture for (A) single feature types, (B) regionalization over different cortical atlases, and (C) independent component analysis features. Refer to Table 2 for a description of each feature set.

Figure 10

Classification accuracy as a function of HCP data release and corresponding multi-modal surface matching algorithm. S500: MSMSulc (Robinson et al., 2014), S1200: MSMAll (Robinson et al., 2018).