Megaripple mechanics: bimodal transport ingrained in bimodal sands
- PMID: 35013166
- PMCID: PMC8748662
- DOI: 10.1038/s41467-021-26985-3
Megaripple mechanics: bimodal transport ingrained in bimodal sands
Abstract
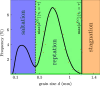
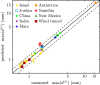
Aeolian sand transport is a major process shaping landscapes on Earth and on diverse celestial bodies. Conditions favoring bimodal sand transport, with fine-grain saltation driving coarse-grain reptation, give rise to the evolution of megaripples with a characteristic bimodal sand composition. Here, we derive a unified phase diagram for this special aeolian process and the ensuing nonequilibrium megaripple morphodynamics by means of a conceptually simple quantitative model, grounded in the grain-scale physics. We establish a well-preserved quantitative signature of bimodal aeolian transport in the otherwise highly variable grain size distributions, namely, the log-scale width (Krumbein phi scale) of their coarse-grain peaks. A comprehensive collection of terrestrial and extraterrestrial data, covering a wide range of geographical sources and environmental conditions, supports the accuracy and robustness of this unexpected theoretical finding. It could help to resolve ambiguities in the classification of terrestrial and extraterrestrial sedimentary bedforms.
© 2022. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures




References
-
- Livingstone, I. & Warren, A. Aeolian Geomorphology: A New Introduction (John Wiley & Sons, 2019).
-
- Pye, K. & Tsoar, H. Aeolian Sand and Sand Dunes (Springer, 2009).
-
- Bagnold, R. The Physics of Blown Sand and Desert Dunes (Methuen, 1941).
-
- Tsoar H. Grain-size characteristics of wind ripples on a desert seif dune. Geogr. Res. Forum. 1990;10:37–50.
-
- Yizhaq H, Isenberg O, Wenkart R, Tsoar H, Karnieli A. Morphology and dynamics of aeolian mega-ripples in Nahal Kasuy, southern Israel. Isr. J. Earth Sci. 2009;57:149–165.
Publication types
LinkOut - more resources
Full Text Sources

