Investigation of biases in convolutional neural networks for semantic segmentation using performance sensitivity analysis
- PMID: 35016819
- PMCID: PMC9948839
- DOI: 10.1016/j.zemedi.2021.11.004
Investigation of biases in convolutional neural networks for semantic segmentation using performance sensitivity analysis
Erratum in
-
Erratum to "Investigation of biases in convolutional neural networks for semantic segmentation using performance sensitivity analysis" [Z Med Phys 32 (2022) 346-360].Z Med Phys. 2025 Feb;35(1):114. doi: 10.1016/j.zemedi.2024.07.007. Epub 2024 Sep 2. Z Med Phys. 2025. PMID: 39227222 Free PMC article. No abstract available.
Abstract
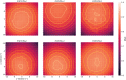
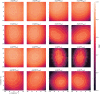
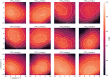
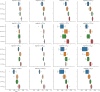
The application of deep neural networks for segmentation in medical imaging has gained substantial interest in recent years. In many cases, this variant of machine learning has been shown to outperform other conventional segmentation approaches. However, little is known about its general applicability. Especially the robustness against image modifications (e.g., intensity variations, contrast variations, spatial alignment) has hardly been investigated. Data augmentation is often used to compensate for sensitivity to such changes, although its effectiveness has not yet been studied. Therefore, the goal of this study was to systematically investigate the sensitivity to variations in input data with respect to segmentation of medical images using deep learning. This approach was tested with two publicly available segmentation frameworks (DeepMedic and TractSeg). In the case of DeepMedic, the performance was tested using ground truth data, while in the case of TractSeg, the STAPLE technique was employed. In both cases, sensitivity analysis revealed significant dependence of the segmentation performance on input variations. The effects of different data augmentation strategies were also shown, making this type of analysis a useful tool for selecting the right parameters for augmentation. The proposed analysis should be applied to any deep learning image segmentation approach, unless the assessment of sensitivity to input variations can be directly derived from the network.
Keywords: Convolutional neural network; Data augmentation; Semantic image segmentation; Sensitivity analysis.
Copyright © 2021. Published by Elsevier GmbH.
Figures
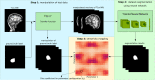

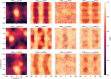
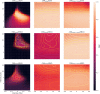
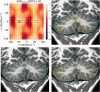
Similar articles
-
[Application of semantic segmentation based on convolutional neural network in medical images].Sheng Wu Yi Xue Gong Cheng Xue Za Zhi. 2020 Jun 25;37(3):533-540. doi: 10.7507/1001-5515.201906067. Sheng Wu Yi Xue Gong Cheng Xue Za Zhi. 2020. PMID: 32597097 Free PMC article. Review. Chinese.
-
A comparison between two semantic deep learning frameworks for the autosomal dominant polycystic kidney disease segmentation based on magnetic resonance images.BMC Med Inform Decis Mak. 2019 Dec 12;19(Suppl 9):244. doi: 10.1186/s12911-019-0988-4. BMC Med Inform Decis Mak. 2019. PMID: 31830973 Free PMC article.
-
Advancing hierarchical neural networks with scale-aware pyramidal feature learning for medical image dense prediction.Comput Methods Programs Biomed. 2025 Jun;265:108705. doi: 10.1016/j.cmpb.2025.108705. Epub 2025 Mar 13. Comput Methods Programs Biomed. 2025. PMID: 40184852
-
Analysis of intensity normalization for optimal segmentation performance of a fully convolutional neural network.Z Med Phys. 2019 May;29(2):128-138. doi: 10.1016/j.zemedi.2018.11.004. Epub 2018 Dec 20. Z Med Phys. 2019. PMID: 30579766
-
Machine learning and image analysis in vascular surgery.Semin Vasc Surg. 2023 Sep;36(3):413-418. doi: 10.1053/j.semvascsurg.2023.07.001. Epub 2023 Jul 7. Semin Vasc Surg. 2023. PMID: 37863613 Review.
Cited by
-
Sensitivity of Diffusion MRI to White Matter Pathology: Influence of Diffusion Protocol, Magnetic Field Strength, and Processing Pipeline in Systemic Lupus Erythematosus.Front Neurol. 2022 Apr 26;13:837385. doi: 10.3389/fneur.2022.837385. eCollection 2022. Front Neurol. 2022. PMID: 35557624 Free PMC article.
References
-
- Anwar S.M., Majid M., Qayyum A., Awais M., Alnowami M., Khan M.K. Medical image analysis using convolutional neural networks: a review. J Med Syst. 2018;42(11):226. - PubMed
-
- Bernal J., Kushibar K., Asfaw D.S., Valverde S., Oliver A., Marti R., et al. Deep convolutional neural networks for brain image analysis on magnetic resonance imaging: a review. Artif Intell Med. 2019;95:64–81. - PubMed
-
- Litjens G., Kooi T., Bejnordi B.E., Setio A.A.A., Ciompi F., Ghafoorian M., et al. A survey on deep learning in medical image analysis. Med Image Anal. 2017;42:60–88. - PubMed
-
- Lundervold A.S., Lundervold A. An overview of deep learning in medical imaging focusing on MRI. Z Med Phys. 2019;29(2):102–127. - PubMed
-
- Maier A., Syben C., Lasser T., Riess C. A gentle introduction to deep learning in medical image processing. Z Med Phys. 2019;29(2):86–101. - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources

