Exploring Transfers between Earth-Moon Halo Orbits via Multi-Objective Reinforcement Learning
- PMID: 35028651
- PMCID: PMC8753611
- DOI: 10.1109/aero50100.2021.9438267
Exploring Transfers between Earth-Moon Halo Orbits via Multi-Objective Reinforcement Learning
Abstract
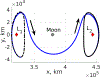
Multi-Reward Proximal Policy Optimization, a multi-objective deep reinforcement learning algorithm, is used to examine the design space of low-thrust trajectories for a SmallSat transferring between two libration point orbits in the Earth-Moon system. Using Multi-Reward Proximal Policy Optimization, multiple policies are simultaneously and efficiently trained on three distinct trajectory design scenarios. Each policy is trained to create a unique control scheme based on the trajectory design scenario and assigned reward function. Each reward function is defined using a set of objectives that are scaled via a unique combination of weights to balance guiding the spacecraft to the target mission orbit, incentivizing faster flight times, and penalizing propellant mass usage. Then, the policies are evaluated on the same set of perturbed initial conditions in each scenario to generate the propellant mass usage, flight time, and state discontinuities from a reference trajectory for each control scheme. The resulting low-thrust trajectories are used to examine a subset of the multi-objective trade space for the SmallSat trajectory design scenario. By autonomously constructing the solution space, insights into the required propellant mass, flight time, and transfer geometry are rapidly achieved.
Figures



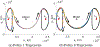
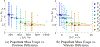
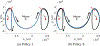
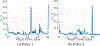
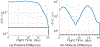
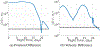
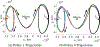
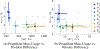
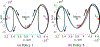
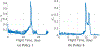
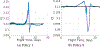

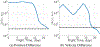
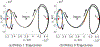
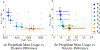
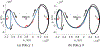
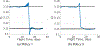
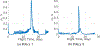
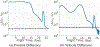
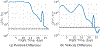
References
-
- Schoolcraft J, Klesh A, and Werne T, “Marco: interplanetary mission development on a cubesat scale,” in Space Operations: Contributions from the Global Community. Springer, 2017, pp. 221–231.
-
- NASA, MarCO (Mars Cube One), 2020, https://solarsystem.nasa.gov/missions/mars-cube-one/in-depth/; Accessed 20 September 2020.
-
- Bosanac N, Cox A, Howell K, and Folta DC, “Trajectory design for a cislunar cubesat leveraging dynamical systems techniques: The lunar icecube mission,” Acta Astronautica, pp. 283–296, 2018.
-
- Genova AL and Dunham DW, “Trajectory design for the lunar polar hydrogen mapper mission,” 27th AAS/AIAA Space Flight Mechanics Meeting, San Antonio, TX, 2017.
-
- Johnson L, Castillo-Rogez J, Dervan J, and McNutt L, “Near earth asteroid (nea) scout,” 4th International Symposium on Solar Sailing, Kyoto Japan, 2017.
Grants and funding
LinkOut - more resources
Full Text Sources
