The evolutionary maintenance of Lévy flight foraging
- PMID: 35041659
- PMCID: PMC8797186
- DOI: 10.1371/journal.pcbi.1009490
The evolutionary maintenance of Lévy flight foraging
Abstract
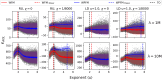
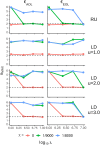
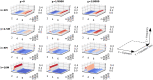
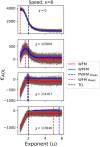
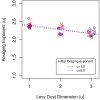
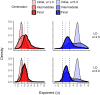
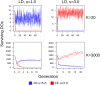
Lévy flight is a type of random walk that characterizes the behaviour of many natural phenomena studied across a multiplicity of academic disciplines; within biology specifically, the behaviour of fish, birds, insects, mollusks, bacteria, plants, slime molds, t-cells, and human populations. The Lévy flight foraging hypothesis states that because Lévy flights can maximize an organism's search efficiency, natural selection should result in Lévy-like behaviour. Empirical and theoretical research has provided ample evidence of Lévy walks in both extinct and extant species, and its efficiency across models with a diversity of resource distributions. However, no model has addressed the maintenance of Lévy flight foraging through evolutionary processes, and existing models lack ecological breadth. We use numerical simulations, including lineage-based models of evolution with a distribution of move lengths as a variable and heritable trait, to test the Lévy flight foraging hypothesis. We include biological and ecological contexts such as population size, searching costs, lifespan, resource distribution, speed, and consider both energy accumulated at the end of a lifespan and averaged over a lifespan. We demonstrate that selection often results in Lévy-like behaviour, although conditional; smaller populations, longer searches, and low searching costs increase the fitness of Lévy-like behaviour relative to Brownian behaviour. Interestingly, our results also evidence a bet-hedging strategy; Lévy-like behaviour reduces fitness variance, thus maximizing geometric mean fitness over multiple generations.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
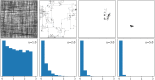

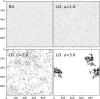
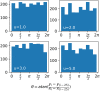
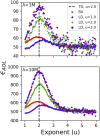


References
-
- Mandelbrot BB. The Fractal Geometry of Nature. Henry Holt and Company; 1983.
-
- Mariani MC, Liu Y. Normalized truncated Levy walks applied to the study of financial indices. Physica A: Statistical Mechanics and its Applications. 2007;377(2):590–598. doi: 10.1016/j.physa.2006.11.066 - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

