Generalised popularity-similarity optimisation model for growing hyperbolic networks beyond two dimensions

Abstract

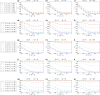
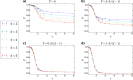
Hyperbolic network models have gained considerable attention in recent years, mainly due to their capability of explaining many peculiar features of real-world networks. One of the most widely known models of this type is the popularity-similarity optimisation (PSO) model, working in the native disk representation of the two-dimensional hyperbolic space and generating networks with small-world property, scale-free degree distribution, high clustering and strong community structure at the same time. With the motivation of better understanding hyperbolic random graphs, we hereby introduce the dPSO model, a generalisation of the PSO model to any arbitrary integer dimension [Formula: see text]. The analysis of the obtained networks shows that their major structural properties can be affected by the dimension of the underlying hyperbolic space in a non-trivial way. Our extended framework is not only interesting from a theoretical point of view but can also serve as a starting point for the generalisation of already existing two-dimensional hyperbolic embedding techniques.

Figure 1

Layouts of networks generated by the dPSO model in 2- and 3-dimensional hyperbolic spaces of curvature $K=-1$. The colouring of the nodes and the links indicates communities found by the Louvain algorithm. In panels a, c, e, g we display the network in the native d-dimensional hyperbolic ball, whereas panels b, d, f, h show the standard Euclidean layout of the same graph for comparison. In the top row, we present networks of the same degree decay exponent $\gamma =2.5$, generated on the 2-dimensional hyperbolic plane, setting the popularity fading parameter $\beta$ to 2/3 (panels a, b), and in the 3-dimensional hyperbolic space, setting the popularity fading parameter $\beta$ to 1/3 (panels c, d). In the bottom row, we show networks of the same popularity fading parameter $\beta =1$, corresponding to the smallest degree decay exponent achievable in a given dimension, namely $\gamma =2.0$ in the 2-dimensional case (panels e, f) and $\gamma =1.5$ in the 3-dimensional case (panels g, h). For each network, we set the number of nodes N to 1000, the expected average degree 2m to 4 and the temperature T to 0. The average clustering coefficient $\overline{c}$ of the displayed networks and the modularity Q for their displayed partitions are the following: $\overline{c}=0.729$ and $Q=0.882$ for panels a, b; $\overline{c}=0.644$ and $Q=0.845$ for panels c, d; $\overline{c}=0.788$ and $Q=0.829$ for panels e, f; while $\overline{c}=0.964$ and $Q=0.354$ for panels g, h.

Figure 2

Degree distribution of networks generated by the dPSO model at different parameter settings. Panels a–e correspond to different dimensions d from 2 to 6. We display in all the panels the complementary cumulative distribution function (CCDF) of the node degrees for networks of two different degree decay exponents: $\gamma =2.5$ (blue) and $\gamma =1+1/(d-1)$ (orange). In both cases, we generated a network using the temperature setting $T=0$ (dashed lines), $T=0.5/(d-1)$ (dash-dotted lines) or $T=1.5/(d-1)$ (dotted lines). The curvature of the hyperbolic space, the number of nodes and the half of the expected average degree were the same for all networks, namely $K=-{\zeta }^2=-1$, $N=10,000$ and $m=2$. All the indicated simulation results match well the curve $\mathcal{P}(k\le K)\sim k^{-(\gamma -1)}$ (shown by solid lines) that was expected based on the analytical calculations.

Figure 3

Average clustering coefficient $\overline{c}$ of dPSO networks as a function of the rescaled temperature $T·(d-1)$. Each row of panels (i.e., panels a–c, d–f, g–i, j–l and m–o) was created using a given dimension d, and each column of subplots presents the results obtained with a given value of the expected average degree 2m, as written in the panel titles. The different curves of each panel correspond to different values of the popularity fading parameter $\beta$ (yielding different degree decay exponents $\gamma$), listed for each dimension in the leftmost panel of the corresponding row. The displayed data points were obtained by averaging over 5 dPSO networks generated independently with a given set of model parameters, setting the number of nodes to 10, 000 and the curvature of the hyperbolic space to $-1$ in each case. The error bars show the standard deviations measured among the 5 networks. The grey vertical lines indicate the critical point $T_{\mathrm{c}}=1/(d-1)$.

Figure 4

Average clustering coefficient $\overline{c}$ measured in d-dimensional PSO networks as a function of the degree decay exponent $\gamma$ at different values of the temperature T and the dimension d. We plotted the average clustering coefficient averaged over 5 networks for each parameter setting, with the error bars indicating the standard deviations among the 5 networks. The size of the networks was $N=10,000$, the expected average degree was $\overline{k}=2m=10$, and each network was generated in a hyperbolic space of curvature $K=-1$. The curves of different colours correspond to different values of the dimension d of the hyperbolic space, listed in the legend. The popularity fading parameter was always set to $\beta =\frac{1}{(d-1)·(\gamma -1)}$. The different panels a–d were created using different values of the temperature T, specified in the panel title.

Figure 5

The highest modularity Q achieved among the communities obtained by the asynchronous label propagation, the Louvain and the Infomap algorithms in dPSO networks, as a function of the rescaled temperature $T·(d-1)$. The dimension d is constant across the panel rows (i.e., in panels a–c, d–f, g–i, j–l and m–o), whereas the expected average degree 2m is constant across the panel columns, as indicated by the panel titles. The different curves in a given subplot correspond to different values of the popularity fading parameter $\beta$ (yielding different degree decay exponents $\gamma$), listed for each dimension in the leftmost panel of the corresponding row. The displayed data points were obtained by averaging over 5 dPSO networks of $N=10,000$ nodes at curvature $K=-{\zeta }^2=-1$, the error bars indicate the standard deviations.

Figure 6

The highest modularity Q achieved between the asynchronous label propagation, the Louvain and the Infomap algorithms in dPSO networks as a function of the degree decay exponent $\gamma$ at different values of the temperature T and the dimension d. The panels a–c refer to different values of the temperature T, given in the title of the subplots. The curves of different colours correspond to different number of dimensions d, as listed below the panels. The popularity fading parameter was calculated as $\beta =\frac{1}{(d-1)·(\gamma -1)}$. We always set the curvature $K=-{\zeta }^2$ of the hyperbolic space to $-1$, the network size N to 10, 000 and the expected average degree 2m to 10. We searched for communities once with all three community detection methods on 5 dPSO networks and plotted the obtained highest modularity averaged over the 5 networks for each parameter setting, with the error bar indicating the standard deviation among the 5 networks.