Quantum logic with spin qubits crossing the surface code threshold

Abstract

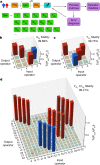
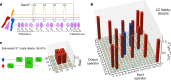
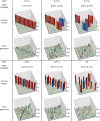
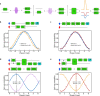
High-fidelity control of quantum bits is paramount for the reliable execution of quantum algorithms and for achieving fault tolerance-the ability to correct errors faster than they occur¹. The central requirement for fault tolerance is expressed in terms of an error threshold. Whereas the actual threshold depends on many details, a common target is the approximately 1% error threshold of the well-known surface code^2,3. Reaching two-qubit gate fidelities above 99% has been a long-standing major goal for semiconductor spin qubits. These qubits are promising for scaling, as they can leverage advanced semiconductor technology⁴. Here we report a spin-based quantum processor in silicon with single-qubit and two-qubit gate fidelities, all of which are above 99.5%, extracted from gate-set tomography. The average single-qubit gate fidelities remain above 99% when including crosstalk and idling errors on the neighbouring qubit. Using this high-fidelity gate set, we execute the demanding task of calculating molecular ground-state energies using a variational quantum eigensolver algorithm⁵. Having surpassed the 99% barrier for the two-qubit gate fidelity, semiconductor qubits are well positioned on the path to fault tolerance and to possible applications in the era of noisy intermediate-scale quantum devices.

Fig. 1. Two-qubit device and symmetry operating point.

a, Scanning electron microscopy images of a device similar to that used here, showing the quantum dot gate pattern and the micromagnet on top (the device used in the experiment has an additional screening gate above the fine gates). The scale bar in the left panel denotes 500 nm. The scale bar in the right panel denotes 100 nm. b, Control paths for determining the symmetry operation point in the charge-stability diagram. (M, N) represent the number of electrons in the dots underneath the tip of LP and RP, respectively. a.u., arbitrary units. c, Pulse sequence schematic of a decoupled controlled-phase operation interleaved in a Ramsey interference sequence on Q₁. d, Spin-up probability of Q₁ after the Ramsey sequence in c, as a function of the detuning in the double-dot potential and the total duration of the barrier voltage pulses.

Fig. 2. Gate-set tomography and single-qubit gate.

a, Workflow of the GST experiment. Coloured blocks show the input and output fiducial sequences (Fid_i and Fid_o, orange) and the germ sequences (green). A few examples of single-qubit germ sequences are listed. The outcome is used to adjust pulse parameters in the next run. b, c, PTMs of ${\mathrm{X}}_{{\mathrm{Q}}_1}$ and ${\mathrm{Y}}_{{\mathrm{Q}}_1}$ in the subspace of Q₁. The red (blue) bars are theoretically +1 (−1) and are measured to be positive (negative). The brown (green) bars are theoretically 0 (0) but measured to be positive (negative). P_in and P_out are the input and output operators, respectively. d, Experimentally measured PTM of ${\mathrm{Y}}_{{\mathrm{Q}}_1}\otimes {\mathrm{I}}_{{\mathrm{Q}}_2}$ in the complete two-qubit space. The colour code is the same as in b, c.

Fig. 3. Hamiltonian engineering of exchange interaction.

a, Frequency detuning of each qubit conditional on the state of the other qubit as a function of barrier pulse amplitude. The horizontal axis shows the real voltage applied to gate B. b, Exchange strength as a function of barrier pulse amplitude. The data are extracted directly from a. c, $T_2^{⁎}$ of each qubit conditional on the state of the other qubit as a function of barrier pulse amplitude (same colour code as in a). Each data point is averaged for about 8 min. By fitting the $T_2^{⁎}$ values to a quasistatic noise model (solid lines, see Methods), the low-frequency amplitudes of the fluctuations are estimated as $\delta f_{{\mathrm{Q}}_1}=11\mathrm{k}\mathrm{H}\mathrm{z}$, $\delta f_{{\mathrm{Q}}_2}=24\mathrm{k}\mathrm{H}\mathrm{z}$ and δv_B = 0.4 mV. d, Shape of the barrier pulse, designed to achieve a high-fidelity CZ gate. e, The cosine-shaped J envelope seen by the qubits during the pulse shown in d.

Fig. 4. High-fidelity two-qubit gate.

a, A sequence of pulses generated by the arbitrary waveform generators in an example GST sequence. The purple waveforms show the in-phase component of X/Y gates. The CZ gate is indicated by the orange pulse of gate B and the blue and red compensation pulses of gate LP and gate RP. b, Experimentally determined PTM of a CZ gate. The colour code is the same as in Fig. 2. c, Left, the quantum circuit used to reconstruct the Bell state $|{\mathrm{\Psi }}^{+}⟩=\left(|01⟩+|10⟩\right)/\sqrt{2}$ based on the corresponding PTMs. Right, the real part of the reconstructed density matrix of the |Ψ⁺⟩ state. The colour code is the same as in Fig. 2, except that red (blue) bars here are theoretically +0.5 (−0.5).

Fig. 5. Variational quantum eigensolver.

a, Lowest two molecular orbitals of a H₂ molecule, formed by the 1s orbitals of two hydrogen atoms. b, The quantum circuit to implement the VQE algorithm for a H₂ molecule. The orange block prepares the HF initial state by flipping Q₂. The circuit in green blocks creates the parameterized ansatz state. $-{\mathrm{X}}_{{\mathrm{Q}}_i}$ and $-{\mathrm{Y}}_{{\mathrm{Q}}_j}$ include virtual Z gates. CNOT gates are compiled as $[-{\mathrm{Y}}_{{\mathrm{Q}}_2},\mathrm{C}\mathrm{Z},{\mathrm{Y}}_{{\mathrm{Q}}_2}]$. To make use of the high-fidelity CZ gate, such compilation is preferred instead of using a single controlled-phase gate with incremental length for creating the parameterized ansatz state. c, Expectation values of the operators in the two-qubit Hamiltonian under BK transformation as a function of θ. Black solid lines show the predicted values. The coloured solid lines are sinusoidal fits to the data (and a constant fit for the case of ZZ). d, Potential energy of the H₂ molecule at varying R. The VQE data are normalized to the theoretical energy at large R to directly compare the dissociation energy with the theoretical value. The inset shows the error in the normalized experimental data.

Extended Data Fig. 1. Two-qubit processes.

Average gate infidelities, process matrices (PTMs) and error generators of the six quantum gates in the chosen gate set. These results are analysed by the pyGSTi package using maximum-likelihood estimation.

Extended Data Fig. 2. Single-qubit processes.

Average gate infidelities and process matrices (PTMs) of the identity gates (idle gates) and single-qubit X/Y gates in the subspace of the individual qubits. The individual PTMs are calculated from the PTMs in the two-qubit space (see Methods).

Extended Data Fig. 3. Bell states predicted from the quantum processes.

Top panels show the real part of the reconstructed density matrices of the four Bell states $|{\mathrm{\Psi }}^{+}⟩=\left(|01⟩+|10⟩\right)/\sqrt{2}$ (a), $|{\mathrm{\Psi }}^{-}⟩=\left(|01⟩-|10⟩\right)/\sqrt{2}$ (b), $|{\mathrm{\Phi }}^{+}⟩=\left(|00⟩+|11⟩\right)/\sqrt{2}$ (c) and $|{\mathrm{\Phi }}^{-}⟩=\left(|00⟩-|11⟩\right)/\sqrt{2}$ (d). The colour code is the same as in Fig. 4. Bottom panels show the quantum circuit used to reconstruct the Bell states. ${\mathrm{Z}}_{\mathrm{Q}i}^2$ is a virtual π-rotation around the $\hat{z}$ axis on the ith qubit, which is executed by a phase update on the microwave reference clock of the qubit and, therefore, is error-free. We numerically estimate the state fidelities to be 98.42% for the |Ψ⁺⟩ and |Ψ⁻⟩ states and 97.75% for the |Φ⁺⟩ and |Φ⁻⟩ states.

Extended Data Fig. 4. Initial gate calibrations.

a, Decomposition of single-qubit and two-qubit gates. After each microwave burst for single-qubit rotations, a corresponding phase correction is applied to each qubit. The CZ gate is implemented by a barrier voltage pulse applied to gate B (orange) and negative compensation pulses applied to gates LP (blue) and RP (red), with the same shape as the barrier pulse. Single-qubit phase corrections are then applied on each qubit to compensate the frequency detuning induced by electron movement in the magnetic field gradient. b, c, Calibration of phase corrections on Q₁ induced by a single-qubit gate applied on Q₂ (ϕ₂₁, b) and on Q₁ (ϕ₁₁, c). A relative phase shift, 2ϕ₂₁ (2ϕ₁₁), is determined by interleaving the target gate (a π/2 rotation) and its inverse (a −π/2 rotation) on Q₂ (Q₁) in a Ramsey interference sequence. d, e, Calibration of phase corrections on each qubit after the CZ gate, using Q₁ (d) and Q₂ (e) as the control qubits, respectively. When the amplitude of the barrier pulse is perfectly calibrated, the two curves in each experiment should be out of phase by 180°. However, when the barrier pulse amplitude is calibrated such that one of the two experiments shows a 180° phase difference (d), the phase difference in the other calibration experiment always deviates by a few degrees. One possible explanation is that the optional π-rotation applied to the control qubit induces a small, off-resonance rotation on the other qubit, causing an additional phase on the target qubit to appear in the measurement due to the commutation relation of the Pauli operators.

Extended Data Fig. 5. Pulse optimization.

a, b, Full error generators for a CZ gate calibrated by conventional Ramsey sequences (a) and after improving the calibration using the information extracted from a (b), resulting in fidelities of 97.86% and 99.65%, respectively. c, d, Seven Hamiltonian errors (IX, IY, XI, YI, IZ, ZI and ZZ) extracted from the error generators shown in a (c) and b (d). Owing to the crosstalk-induced additional phases shown in Extended Data Fig. 4, errors IZ, ZI and ZZ occur systematically in conventional calibrations. Error bars indicate the 2σ confidence intervals computed using the Hessian of the loglikelihood function. e, f, Shapes of the barrier pulses (e) and their corresponding J envelopes (f) for a CZ gate before and after being corrected by GST. Since the Hamiltonian to generate a CZ gate is H = (II + IZ + ZI − ZZ)/2, the positive ZZ error shown in c is corrected by increasing the amplitude of the pulse. The IZ and ZI errors are corrected by decreasing the phase shifts θ₁ and θ₂ after the CZ gate. Hamiltonian errors in single-qubit gates are corrected similarly. The results presented in b and d are achieved in four loops of correction, with each loop correcting the parameters by approximately 70% of the measured deviation.

Extended Data Fig. 6. Workflow of the variational quantum eigensolver algorithm.

The qubit Hamiltonian is typically transformed from the molecular Hamiltonian by JW transformation or BK transformation by a classical processor (see Methods). A HF initial state is encoded into the qubit states according to JW or BK transformation and then transformed by the quantum processor into a parameterized ansatz state by considering single and double excitation in the molecule using the UCC theory. The expectation value of each individual Hamiltonian term is directly measured by partial state tomography. The expectation of the total energy is then calculated by the weighted sum of the individual expectations. The result is fed into a classical optimizer, which suggests a new parameterized ansatz state for the next run. This process is repeated until the expectation of the total energy converges.