Dynamic Modeling and Experimental Validation of a Water Hydraulic Soft Manipulator Based on an Improved Newton-Euler Iterative Method
- PMID: 35056295
- PMCID: PMC8778452
- DOI: 10.3390/mi13010130
Dynamic Modeling and Experimental Validation of a Water Hydraulic Soft Manipulator Based on an Improved Newton-Euler Iterative Method
Abstract
Compared with rigid robots, soft robots have better adaptability to the environment because of their pliability. However, due to the lower structural stiffness of the soft manipulator, the posture of the manipulator is usually decided by the weight and the external load under operating conditions. Therefore, it is necessary to conduct dynamics modeling and movement analysis of the soft manipulator. In this paper, a fabric reinforced soft manipulator driven by a water hydraulic system is firstly proposed, and the dynamics of both the soft manipulator and hydraulic system are considered. Specifically, a dynamic model of the soft manipulator is established based on an improved Newton-Euler iterative method, which comprehensively considers the influence of inertial force, elastic force, damping force, as well as combined bending and torsion moments. The dynamics of the water hydraulic system consider the effects of cylinder inertia, friction, and water response. Finally, the accuracy of the proposed dynamic model is verified by comparing the simulation results with the experimental data about the steady and dynamic characteristics of the soft manipulator under various conditions. The results show that the maximum sectional error is about 0.0245 m and that the maximum cumulative error is 0.042 m, which validate the effectiveness of the proposed model.
Keywords: Newton–Euler iterative method; dynamic modeling; soft manipulator; water hydraulic system.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
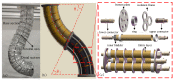
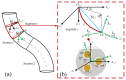
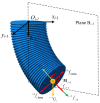
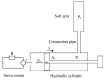
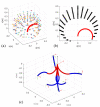

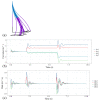
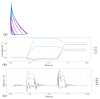


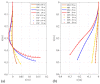


References
-
- Wang T., Hao Y., Yang X., Wen L. Soft robotics: Structure, actuation, sensing and control. J. Mech. Eng. 2017;53:1–13.
-
- Wang H., Peng X., Lin B. Research development of soft robots. J. S. China Univ. Technol. 2020;48:98–110.
-
- Cao Y., Shang J., Liang K., Fan D., Ma D., Tang L. Review of soft-bodied robots. J. Mech. Eng. 2012;48:9. doi: 10.3901/JME.2012.03.025. - DOI
-
- Yan J., Shi P., Zhang X., Zhao J. Review of biomimetic mechanism, actuation, modeling and control in soft manipulator. J. Mech. Eng. 2018;54:1–14. doi: 10.3901/JME.2018.15.001. - DOI
-
- Yu J., Hao G., Chen G., Bi S. State-of-art of compliant mechanisms and their applications. J. Mech. Eng. 2015;51:53–68. doi: 10.3901/JME.2015.13.053. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

