Impurity-Induced Magnetization of Graphene

Abstract

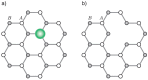
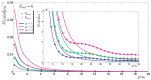
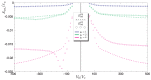
We present a model of impurity-induced magnetization of graphene assuming that the main source of graphene magnetization is related to impurity states with a localized spin. The analysis of solutions of the Schrödinger equation for electrons near the Dirac point has been performed using the model of massless fermions. For a single impurity, the solution of Schrödinger's equation is a linear combination of Bessel functions. We found resonance energy levels of the non-magnetic impurity. The magnetic moment of impurity with a localized spin was accounted for the calculation of graphene magnetization using the Green's function formalism. The spatial distribution of induced magnetization for a single impurity is obtained. The energy of resonance states was also calculated as a function of interaction. This energy is depending on the impurity potential and the coupling constant of interaction.

Keywords: graphene; impurity; localized states; magnetism; resonant states; spintronics.

Figure 1

(a) First Brillouin zone in graphene with marked points, (b) Γ—center of the zone, M—center of the edge, K and $K^{\prime }$ are the nonequivalent Dirac points.

Figure 2

Single-node doping in graphene, (a) a new atom instead of a carbon atom, (b) a gap in the graphene lattice.

Figure 3

Dependence of resonant energy levels $\epsilon$ of a state localized on a non-magnetic impurity with the potential $V_0$ Equation (16), where ${\epsilon }_c={\hslash }^2/\left(m_e{a}_0^2\right)$, $V_c={\epsilon }_c{a}_0^2$, $m_e$ is the mass of electron, and $a_0$ is the distance between carbon atoms. Localized states without magnetic correlations.

Figure 4

Induced local magnetization $M_z\left(\varrho \right)$ as a function of the distance from the impurity center $\varrho$.

Figure 5

Interaction energy $E_{int}$ as the function of impurity potential $V_0$. ×—the results obtained for the interaction energy in the first iteration step (see the blue dashed line (Figure 6)). Solutions marked with a circles correspond to $E_{int}$ in the last iteration step of the self-reconciliation procedure. Colors denote different values of the constant $g_c$.

Figure 6

Resonant energy levels $\epsilon$ with consideration of magnetic interaction $E_{int}$ as a function of renormalized impurity potential $V_0$ for different values of coupling constant $g_c$.