Epidemic dynamics on higher-dimensional small world networks

Abstract

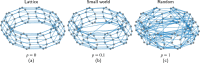
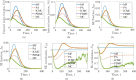
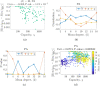
Dimension governs dynamical processes on networks. The social and technological networks which we encounter in everyday life span a wide range of dimensions, but studies of spreading on finite-dimensional networks are usually restricted to one or two dimensions. To facilitate investigation of the impact of dimension on spreading processes, we define a flexible higher-dimensional small world network model and characterize the dependence of its structural properties on dimension. Subsequently, we derive mean field, pair approximation, intertwined continuous Markov chain and probabilistic discrete Markov chain models of a COVID-19-inspired susceptible-exposed-infected-removed (SEIR) epidemic process with quarantine and isolation strategies, and for each model identify the basic reproduction number $R_0$ , which determines whether an introduced infinitesimal level of infection in an initially susceptible population will shrink or grow. We apply these four continuous state models, together with discrete state Monte Carlo simulations, to analyse how spreading varies with model parameters. Both network properties and the outcome of Monte Carlo simulations vary substantially with dimension or rewiring rate, but predictions of continuous state models change only slightly. A different trend appears for epidemic model parameters: as these vary, the outcomes of Monte Carlo change less than those of continuous state methods. Furthermore, under a wide range of conditions, the four continuous state approximations present similar deviations from the outcome of Monte Carlo simulations. This bias is usually least when using the pair approximation model, varies only slightly with network size, and decreases with dimension or rewiring rate. Finally, we characterize the discrepancies between Monte Carlo and continuous state models by simultaneously considering network efficiency and network size.

Keywords: Epidemic spreading; Model error; Network dimension; Small world model; Spreading dynamics.

Fig. 1

Regular lattices of (mean) degree $〈k〉=10$ and dimension (a) $D=1$, (b) $D=2$, (c) $D=3$, (d) $D=4$ and (e) $D=5$. The subgraph induced by a node and its neighbours is shown with larger, black nodes and thicker, red links. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 2

Using the small world network with random rewiring to interpolate between a two-dimensional lattice (rewiring rate $p=0$) and a random network ($p=1$). Network size $N=100$ and mean degree $〈k〉=4$.

Fig. 3

Using the small world network with distance dependent rewiring to interpolate between a two-dimensional lattice (rewiring rate $p=0$) and a random network ($p=1$). The probability for a node to be a recipient of a rewired link decreases with the periodic Euclidean lattice distance $d_2$ as ${d_2}^{-3}$ (Section 2.2). Network size $N=100$ and mean degree $〈k〉=4$.

Fig. 4

Structural properties of regular lattices networks depend on dimension $D$ and mean degree $〈k〉$. (a) Variation with dimension $D$ of clustering coefficient $\varphi$, network efficiency $\eta$, and mean network distance $〈d〉$, for regular lattices with (mean) degree $〈k〉=10$ and about $N=3,000$ nodes. (b) Variation with (mean) degree $〈k〉$ of clustering coefficient $\varphi$, network efficiency $\eta$, and mean network distance $〈d〉$, for regular lattices of dimension $D=2$ with $N=3,025$ nodes.

Fig. 5

Network structural properties depend on rewiring rate $p$ and rewiring strategy. For a network with dimension $D=2$, mean degree $〈k〉=10$ and $N=3,025$ nodes, variation with random and distance dependent rewiring rate $p$ of: (a) clustering coefficient $\varphi$ and network efficiency $\eta$; and (b) mean network distance $〈d〉$. For networks of five different dimensions, size about $N=3,000$ and mean degree $〈k〉=10$, the largest eigenvalue ${\Lambda }_1$, second largest eigenvalue ${\Lambda }_2$ and negative $-{\Lambda }_N$ of the smallest eigenvalue under: (c) random rewiring; and (d) distance dependent rewiring. The values of ${\Lambda }_1$, ${\Lambda }_2$ and $-{\Lambda }_N$ shown comprise the mean over twenty independently generated graphs.

Fig. 6

Access to higher dimensions improves fitting to topological properties and prediction of dynamical properties. Errors in fitting and prediction of properties of eighty-four US high school friendship networks (Table 1) . (a) Error $F$ in fitted, topological properties, calculated using Eq. (1). (b) Error $P$ in predicted, dynamical properties calculated using Eq. (2). The original small world network model is restricted to dimension $D=1$, but the higher-dimensional network model allows the use of a the fitted dimension $D=\widehat{D}$. The number of times each approach is optimal (Opt.) and yields the (possibly equal) lowest error is shown in the legends. For readability, the observed real worlds networks are ordered, separately for (a) and (b), by increasing error in the $D=1$ case.

Fig. 7

Structure of the SEIR disease spreading model. ${\lambda }_1$: infection rate from E nodes; ${\lambda }_2$: infection rate from I nodes; $\mu$: disease progression rate; $\xi$: quarantine rate; $\gamma$: recovery rate; $\delta$: isolation rate.

Fig. 8

Different descriptions of the SEIR spreading process predict distinct time evolution. Variation with time $t$ according to five different methods: MF, PA, ICMC, PDMC and MC. (a) Exposed node fraction $E\left(t\right)$; (b) infected node fraction $I\left(t\right)$; (c) SE pair fraction ${\rho }_{SE}$; (d) SI pair fraction ${\rho }_{SI}$; (e) SE correlation $C_{SE}$; and (f) SI correlation $C_{SI}$. Spreading takes place on a small world network with size $N=3,025$, dimension $D=2$, mean degree $〈k〉=10$ and random rewiring rate $p=0.01$.

Fig. 9

The final number affected by the disease increases with infection rate. (a)–(e) Variation with infection rates ${\lambda }_1$ and ${\lambda }_2$ of the final affection ratio $R\left(\infty \right)$ when using the (a) MF; (b) PA; (c) ICMC; (d) PDMC; and (e) MC methods. Level sets of the final affected density $R\left(\infty \right)$ are shown with black dashed lines, while the white dotted line highlights parameters for which the basic reproduction number $R_0$ is unity. (f) Variation with ${\lambda }_2$ of the final affection ratio $R\left(\infty \right)$, with ${\lambda }_1=0.005$. Spreading takes place on a small world network with dimension $D=2$, size $N=3,025$, mean degree $〈k〉=10$ and random rewiring rate $p=0.01$. Results for Monte Carlo comprise the mean over twenty independent trials.

Fig. 10

The final number affected by the disease decreases with quarantine rate $\xi$ and isolation rate $\delta$. Variation of final affected ratio $R\left(\infty \right)$ with (a) quarantine rate $\xi$ and (b) isolation rate $\delta$ for a small world network of dimension $D=2$, size $N=3,025$, mean degree $〈k〉=10$ and random rewiring rate $p=0.01$.

Fig. 11

The final number affected by the disease increases with mean degree. (a-e) Variation with mean degree $〈k〉$ of the final affected ratio $R\left(\infty \right)$ according to the MF, PA, ICMC, PDMC and MC methods for networks of size about $N=3,000$, randomly rewired with probability $p=0.01$, and with dimension (a) $D=1$, (b) $D=2$, (c) $D=3$, (d) $D=4$, and (e) $D=5$. (f) The difference between MC and other methods for the network of dimension $D=2$.

Fig. 12

The final number affected by the disease increases with rewiring rate $p$, but this variation decreases with dimension $D$. Change with rewiring rate $p$ of affected node fraction $R\left(\infty \right)$ for networks with mean degree $〈k〉=10$ and $N=3,025$ nodes: (a,b) in dimension $D=2$ using MF, PA, ICMC, PDMC and MC methods; and (c,d) using MC in dimensions $D=1$ to 5. Rewiring is: (a,c) random; and (b,d) distance dependent.

Fig. 13

The final number affected by the disease varies little with network size $N$. Variation with network size $N$ of affected node fraction $R\left(\infty \right)$ using MF, PA, ICMC, PDMC and MC methods, for networks with dimension, mean degree and random rewiring rate: (a) $D=1$, $〈k〉=4$ and $p=1$; (b) $D=2$, $〈k〉=10$ and $p=0.01$; and (c) $D=4$, $〈k〉=20$ and $p=0.1$. .

Fig. 14

For fixed (combined) mean degree $〈k〉$, the discrepancy between PA and MC decreases (increases) with increasing capacity $\chi$. Variation with different network properties of the absolute value of the difference between the mean affected ratio for PA and MC methods for random small world networks of size between about ${\tilde{N}}_{\min }=500$ and ${\tilde{N}}_{\max }=10,000$ and rewiring rate bounded below by $p_{\min }={10}^{-4}$. (a) For fixed mean degree $〈k〉=10$, variation of the absolute value of the difference versus capacity $\chi$. (b) Kendall $\tau$ correlation between absolute deviation and network size $N$, efficiency $\eta$ and capacity $\chi$ respectively versus mean degree $〈k〉$ and (c) levels of significance for hypothesis that error decreases with these network properties. (d) Absolute value of the difference between the mean affected ratio for PA and MC methods versus network capacity $\chi$, with all mean degrees $〈k〉$ combined.

Fig. 15

For fixed (combined) mean degree $〈k〉$, the discrepancy between MF and MC decreases (increases) with increasing efficiency $\eta$. Variation with different network properties of the absolute value of the difference between the mean affected ratio for MF and MC methods for random small world networks with size between about ${\tilde{N}}_{\min }=500$ and ${\tilde{N}}_{\max }=10,000$ and rewiring rate bounded below by $p_{\min }={10}^{-4}$ (Section 2.2). (a) For fixed mean degree $〈k〉=10$, variation of the absolute value of the difference versus efficiency $\eta$. (b) Kendall $\tau$ correlation between absolute deviation and network size $N$, efficiency $\eta$ and capacity $\chi$ respectively versus mean degree $〈k〉$ and (c) levels of significance for the hypothesis that error decreases with these network properties. (d) Absolute value of the difference between the mean affected ratio for MF and MC methods versus network efficiency $\eta$, with all mean degrees $〈k〉$ combined.