Deriving the Bidomain Model of Cardiac Electrophysiology From a Cell-Based Model; Properties and Comparisons

Abstract

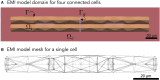
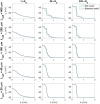
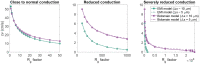
The bidomain model is considered to be the gold standard for numerical simulation of the electrophysiology of cardiac tissue. The model provides important insights into the conduction properties of the electrochemical wave traversing the cardiac muscle in every heartbeat. However, in normal resolution, the model represents the average over a large number of cardiomyocytes, and more accurate models based on representations of all individual cells have therefore been introduced in order to gain insight into the conduction properties close to the myocytes. The more accurate model considered here is referred to as the EMI model since both the extracellular space (E), the cell membrane (M) and the intracellular space (I) are explicitly represented in the model. Here, we show that the bidomain model can be derived from the cell-based EMI model and we thus reveal the close relation between the two models, and obtain an indication of the error introduced in the approximation. Also, we present numerical simulations comparing the results of the two models and thereby highlight both similarities and differences between the models. We observe that the deviations between the solutions of the models become larger for larger cell sizes. Furthermore, we observe that the bidomain model provides solutions that are very similar to the EMI model when conductive properties of the tissue are in the normal range, but large deviations are present when the resistance between cardiomyocytes is increased.

Keywords: EMI model; bidomain model; cardiac conduction; cardiac electrophysiology; cardiac tissue models; cell-based model; numerical simulation.

Figure 1

(A) Illustration of an EMI model domain for four connected cells. The intracellular space (orange) is denoted by Ω_i and the extracellular space (red) is denoted by Ω_e. The cell membrane is defined as the interface between the intracellular and extracellular spaces and is denoted by Γ. Similarly, the intercalated discs (purple) are denoted by Γ_g and are defined as the interface between neighboring cells. Each cell is shaped as a cylinder with a diameter increasing slightly toward the center of the cell. (B) Illustration of the finite element mesh used to represent a single cell in the EMI model simulations.

Figure 2

Illustration of a tissue block, Δ, containing a number of cells (orange) and a surrounding extracellular space (red). In Step 1 of the derivation we approximate the discontinuous intracellular space (A) consisting of individual cells connected by gap junctions by a continuous intracellular space (B).

Figure 3

Intracellular potential, u_i, at time t = 20 ms in EMI model and bidomain model simulations using a passive membrane model (Equation 74) and the default parameter values specified in Table 1, except that the value of R_g is increased by the factor indicated by the column titles. In addition, the cell length (L_cell) is varied as described for each row of plots.

Figure 4

Conduction velocity as R_g is increased in EMI model and bidomain model simulations of a strand of 20 connected cells with an active membrane model (Jæger et al., 2021b). The values on the x-axis represent the factor with which the default R_g value in Table 1 is multiplied. The remaining parameter values are as specified in Table 1. Note that the plot is separated into three panels in order to improve the visibility of the data. Note also that we consider two different discretization resolutions in the simulations of each model. In the default case, Δt = 0.001 ms and Δx in the bidomain model and the typical edge length in the EMI model is 10 μm, whereas in the refined case (dashed lines), both the spatial and temporal discretization steps are reduced to half of the default values.

Figure 5

Membrane potential, v, and extracellular potential, u_e, at time t = 5 ms in EMI model and bidomain model simulations using the default parameter values specified in Table 1 and an active membrane model (Jæger et al., 2021b). This simulation required a CPU time of 132 min for the EMI model and 2 min for the bidomain model.

Figure 6

Membrane potential, v, and extracellular potential, u_e, at time t = 20 ms in EMI model and bidomain model simulations using and active membrane model (Jæger et al., 2021b) and the default parameter values specified in Table 1, except that the value of R_g is increased by a factor of 200.