A stochastically curtailed single-arm phase II trial design for binary outcomes

Abstract

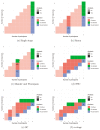
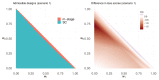
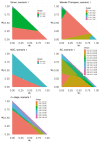
Phase II clinical trials are a critical aspect of the drug development process. With drug development costs ever increasing, novel designs that can improve the efficiency of phase II trials are extremely valuable.Phase II clinical trials for cancer treatments often measure a binary outcome. The final trial decision is generally to continue or cease development. When this decision is based solely on the result of a hypothesis test, the result may be known with certainty before the planned end of the trial. Unfortunately, there is often no opportunity for early stopping when this occurs.Some existing designs do permit early stopping in this case, accordingly reducing the required sample size and potentially speeding up drug development. However, more improvements can be achieved by stopping early when the final trial decision is very likely, rather than certain, known as stochastic curtailment. While some authors have proposed approaches of this form, these approaches have various limitations.In this work we address these limitations by proposing new design approaches for single-arm phase II binary outcome trials that use stochastic curtailment. We use exact distributions, avoid simulation, consider a wider range of possible designs and permit early stopping for promising treatments. As a result, we are able to obtain trial designs that have considerably reduced sample sizes on average.

Keywords: Adaptive design; cancer; continuous monitoring; interim analysis; oncology.

Figure 1

Illustrative diagrams of different trial designs, showing potential points where the study would end, known as terminal points. m: Number of participant results so far. S(m): Number of responses so far. All trials have N = 8, r = 4, with r₁ = 1 in the two-stage designs and e₁ = 3 in Mander and Thompson’s design. We may assume that (θ_F, θ_E) in the SC design are such that (e₅, e₆, e₇, e₈) = (5, 5, 5, 5), (f₂, f₄, f₆, f₇, f₈) = (0, 1, 2, 3, 4) and that (θ_F, θ_E) in the m-stage design are such that (e₄, e₅, e₇, e₈) = (4, 4, 5, 5), (f₂, f₃, f₆, f₇, f₈) = (0, 1, 2, 3, 4).

Figure 2

CC: Chi and Chen. AR: Ayanlowo and Redden. KK: Kunz and Kieser. *The approach of Ayanlowo and Redden uses θ_F ∈ {0.05, 0.10}. **The approach of Kunz and Kieser uses θ_F ∈ {0, 0.01, …, 1}.

Figure 3

Type of design to which the omni-admissible design realisation belongs and difference in loss scores between the SC and m-stage admissible design realisations (positive favours m-stage), scenario 1 (α, β, p₀, p₁) = (0.05, 0.15, 0.10, 0.30).

Figure 4

Admissible design realisations for scenario 1 (α, β, p₀, p₁) = (0.05, 0.15, 0.10, 0.30). Format of design realisations: Simon, NSC: {r₁/n₁, r/N}; Mander and Thompson: {(r₁ e₁)/n₁, r/N}; SC: {r₁/n₁, r/N, θ_F/θ_E}; m-stage: {r/N, θ_F/θ_E}.

Figure 5. Bias, RMSE for p₀-optimal designs, scenario 1 (α, β, p₀, p₁) = (0.05, 0.15, 0.10, 0.30).

Figure 6. Bias, RMSE for p₀-optimal designs, scenario 1 (α, β, p₀, p₁) = (0.05, 0.15, 0.10, 0.30), continued.