The boundary for quantum advantage in Gaussian boson sampling

Abstract

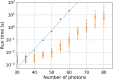
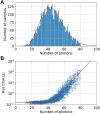
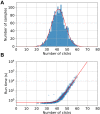
Identifying the boundary beyond which quantum machines provide a computational advantage over their classical counterparts is a crucial step in charting their usefulness. Gaussian boson sampling (GBS), in which photons are measured from a highly entangled Gaussian state, is a leading approach in pursuing quantum advantage. State-of-the-art GBS experiments that run in minutes would require 600 million years to simulate using the best preexisting classical algorithms. Here, we present faster classical GBS simulation methods, including speed and accuracy improvements to the calculation of loop hafnians. We test these on a ∼100,000-core supercomputer to emulate GBS experiments with up to 100 modes and up to 92 photons. This reduces the simulation time for state-of-the-art GBS experiments to several months, a nine-orders of magnitude improvement over previous estimates. Last, we introduce a distribution that is efficient to sample from classically and that passes a variety of GBS validation methods.

Fig. 1.. Conceptual schematic of repeated-row loop hafnian algorithm and threshold detector sampling method.

(A) A GBS outcome with collisions, measured with PNRDs. (B) To calculate the associated probability, we group the photons into pairs (red lines) to maximize the number of repeated, identical pairs. (C) An inclusion/exclusion formula, or a finite-difference sieve, can then operate on the resulting pairs, with repeated pairs leading to a speedup. (D) The same event measured with threshold detectors, with “clicks” shown as green ticks. (E) We consider a fan-out to an array of subdetectors, with none likely to receive >1 photon. We can ignore the outcomes of all but the first detector to see a photon. x is introduced as the relative position of the detected photon and is also the fraction of the subdetectors that are ignored. (F) The probability of detecting the first photon at position x can be expressed as a loss followed by single-photon detection.

Fig. 2.. Theoretical and sample-estimated GBS probability distributions.

Probability distribution for all six-photon detection outcomes for an eight-mode PNRD GBS simulation (A) and an eight-mode, three-click threshold detector GBS simulation (B). Blue bars show estimated probabilities using MIS; orange bars show exact probabilities.

Fig. 3.. Loop hafnian run time benchmarking.

Run time using the HPE benchmarking system, comparing eigenvalue trace loop hafnian algorithm on N × N matrices with and without speedup due to collisions (orange and blue dots). The blue line is an exponential fitted to the blue points. Collisions are determined by generating 39 samples for each N from the IPS distribution on 60 modes.

Fig. 4.. Chain rule benchmarking on 60-mode PNRD GBS.

Chain rule simulation of M = 60 experiment with PNRDs. (A) Number of samples as a function of photon number, with the theoretically calculated distribution (red line) and (B) run time versus number of photons fitted with an exponential plus a constant (red line).

Fig. 5.. Chain rule benchmarking on 100-mode threshold detector GBS.

Chain rule simulation of M = 100 experiment with threshold detectors. (A) Number of samples as a function of number of clicks, fitted with a Gaussian (red line). (B) Run time versus number of clicks, fitted with an exponential plus a constant (red line).