Infection dynamics of COVID-19 virus under lockdown and reopening

Abstract

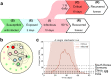
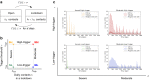
Motivated by COVID-19, we develop and analyze a simple stochastic model for the spread of disease in human population. We track how the number of infected and critically ill people develops over time in order to estimate the demand that is imposed on the hospital system. To keep this demand under control, we consider a class of simple policies for slowing down and reopening society and we compare their efficiency in mitigating the spread of the virus from several different points of view. We find that in order to avoid overwhelming of the hospital system, a policy must impose a harsh lockdown or it must react swiftly (or both). While reacting swiftly is universally beneficial, being harsh pays off only when the country is patient about reopening and when the neighboring countries coordinate their mitigation efforts. Our work highlights the importance of acting decisively when closing down and the importance of patience and coordination between neighboring countries when reopening.

Figure 1

The disease spread without an intervention. (a) Two days after being exposed to the disease (E), the individual becomes infectious (I) as they develop mild condition. If a critical condition develops (C), the individual is hospitalized and isolated. We assume that all surviving individuals (R) acquire immunity. (b) A population of N individuals. Each day, an individual meets k other individuals. During a single meeting with an infectious person, a susceptible individual contracts a disease with a transmission probability p. (c) Without intervention, the disease surges through the community and the critical cases (curve) at its peak $C_{\text{max}}$ exceed the available hospital bed capacity $c$ (dashed lines^,). Here $N=1000$, $k=15$, $p=2\%$, thus the effective reproductive rate $R_e$ is roughly $R_e\doteq 2.9$.

Figure 2

Basic policies. (a) Under a policy $P(\tau ,k,d)$, the country locks down to $k<k_0$ daily contacts whenever the number C(t) of critical cases exceeds a trigger threshold $\tau$. It reopens (to $k_0$ daily contacts) once the number of critical cases stays below $\tau$ for $d$ consecutive days. (b) We consider four different policies given by a combination of a trigger threshold (low trigger ${\tau }_{\text{low}}=3$, high trigger ${\tau }_{\text{high}}=12$) and a lockdown severity (severe $k_{\text{low}}=1.25$, moderate $k_{\text{high}}=6$), and common patience $d=10$ days. (c) Representative runs under the four policies (for 800 days). While with the severe high-trigger policy $P_{\mathit{SH}}$ (top left) all peaks are similar in shape, with the moderate low-trigger policy $P_{\mathit{ML}}$ (bottom right) all subsequent peaks are much smaller than the first one. With the moderate high-trigger policy $P_{\mathit{MH}}$ (top right) the capacity is exceeded and with the severe low-trigger policy $P_{\mathit{SL}}$ (bottom left) the disease is quickly eradicated.

Figure 3

Performance of low-trigger and high-trigger policies. The four performance measures: (a) average peak size $C_{\text{max}}$, (b) overflow probability $p_{\text{fail}}$, (c) total critical cases $C_{\text{all}}$, and (d) lockdown duration $D$ (${10}^5$ runs). In each panel, we vary the number $k$ of daily contacts (x-axis) and consider the performance (cost) of the low-trigger policies (${\tau }_{\text{low}}=3$, blue) and of the high-trigger policies (${\tau }_{\text{high}}=12$, green), when the patience parameter is low ($d=7$ days, left column) and high ($d=70$, right column). The dotted red line shows the number $k^{\star }$ of daily contacts that corresponds to the effective reproductive rate $R_e$ equal to 1 (when no individuals have yet recovered). Generally speaking, it is beneficial to have the trigger value $\tau$ low (blue curves are below green ones), to impose severe rather than moderate lockdown (all curves are increasing functions of k for $k\le k^{\star }$), and to be patient (the curves in the right panels are lower). For $C_{\text{max}}$ and $p_{\text{fail}}$, the key is to have the trigger value $\tau$ low. For $C_{\text{all}}$ and $D$, the key is to have the patience $d$ high.

Figure 4

Two countries. (a) When two countries interact with a positive rate $q$ they might reinfect each other. Here $q=5·{10}^{-4}$, and the countries employ different policies: $P_{\mathit{ML}}$ (blue) and $P_{\mathit{SH}}$ (yellow). (b) A $90\%$ percentile: on any given day, 90% of the runs are below the respective curves (${10}^5$ runs). (c–f) The performance of a $P_{\mathit{ML}}$ policy against a $P_{\mathit{SH}}$ policy (blue), $P_{\mathit{SH}}$ vs. $P_{\mathit{ML}}$ (green), $P_{\mathit{ML}}$ vs. $P_{\mathit{ML}}$ (yellow) and $P_{\mathit{SH}}$ vs. $P_{\mathit{SH}}$ (red), averaged over ${10}^4$ runs. We vary the interaction rate $q$ on a log-scale and measure: (c) the overflow probability $p_{\text{fail}}$ (95% confidence intervals are shaded); (d) the expected peak size $C_{\text{max}}$; (e) the total number $C_{\text{all}}$ of critical cases; and (f) the lockdown duration $D$. A country employing $P_{\mathit{SH}}$ does great when its neighbor employs $P_{\mathit{SH}}$ (red) but bad when the neighbor employs $P_{\mathit{ML}}$ (green). A country employing $P_{\mathit{ML}}$ does comparably well, regardless of whether the neighbor employs $P_{\mathit{ML}}$ (yellow) or $P_{\mathit{SH}}$ (blue).