Tensile fatigue strength and endurance limit of human meniscus
- PMID: 35091175
- PMCID: PMC9925119
- DOI: 10.1016/j.jmbbm.2021.105057
Tensile fatigue strength and endurance limit of human meniscus
Abstract
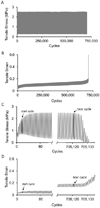
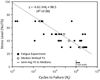
The knee menisci are prone to mechanical fatigue injury from the cyclic tensile stresses that are generated during daily joint loading. Here we characterize the tensile fatigue behavior of human medial meniscus and investigate the effect of aging on fatigue strength. Test specimens were excised from the medial meniscus of young (under 40 years) and older (over 65 years) fresh-frozen cadaver knees. Cyclic uniaxial tensile loads were applied parallel to the primary circumferential fibers at 70%, 50%, 40%, or 30% of the predicted ultimate tensile strength (UTS) until failure occurred or one million cycles was reached. Equations for fatigue strength (S-N curve) and the probability of fatigue failure (unreliability curves) were created from the measured number of cycles to failure. The mean number of cycles to failure at 70%, 50%, 40%, and 30% of UTS were estimated to be approximately 500, 40000, 340000, and 3 million cycles, respectively. The endurance limit, defined as the tensile stress that can be safely applied for the average lifetime of use (250 million cycles), was estimated to be 10% of UTS (∼1.0 MPa). When cyclic tensile stresses exceeded 30% of UTS (∼3.0 MPa), the probability of fatigue failure rapidly increased. While older menisci were generally weaker and more susceptible to fatigue failures at high-magnitude tensile stresses, both young and older age groups had similar fatigue resistance at low-magnitude tensile stresses. In addition, we found that fatigue failures occurred after the dynamic modulus decreased during cyclic loading by approximately 20%. This experimental study has quantified fundamental fatigue properties that are essential to properly predict and prevent injury in meniscus and other soft fibrous tissues.
Keywords: Damage; Effect of Aging; Fatigue life; Mechanical properties; Probability of Fatigue Failure; Soft tissue.
Copyright © 2022 Elsevier Ltd. All rights reserved.
Figures
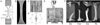






References
-
- Alam P, Mamalis D, Robert C, Floreani C, Ó Brádaigh CM, 2019. The fatigue of carbon fibre reinforced plastics - A review. Composites Part B: Engineering 166, 555–579. 10.1016/j.compositesb.2019.02.016 - DOI
-
- ASTM, 2017. Test Method for Uniaxial Fatigue Properties of Plastics. ASTM International. 10.1520/D7791-17 - DOI
-
- Budynas R, Nisbett K, 2014. Shigley’s Mechanical Engineering Design, 10th edition. ed. McGraw-Hill Education, New York, NY.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

