Puff turbulence in the limit of strong buoyancy

Abstract

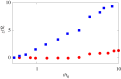
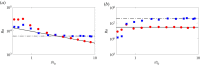
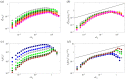
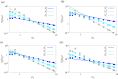
We provide a numerical validation of a recently proposed phenomenological theory to characterize the space-time statistical properties of a turbulent puff, both in terms of bulk properties, such as the mean velocity, temperature and size, and scaling laws for velocity and temperature differences both in the viscous and in the inertial range of scales. In particular, apart from the more classical shear-dominated puff turbulence, our main focus is on the recently discovered new regime where turbulent fluctuations are dominated by buoyancy. The theory is based on an adiabaticity hypothesis which assumes that small-scale turbulent fluctuations rapidly relax to the slower large-scale dynamics, leading to a generalization of the classical Kolmogorov and Kolmogorov-Obukhov-Corrsin theories for a turbulent puff hosting a scalar field. We validate our theory by means of massive direct numerical simulations finding excellent agreement. This article is part of the theme issue 'Scaling the turbulence edifice (part 2)'.

Keywords: intermittency; non-ideal turbulence; scaling in turbulence.

Figure 1.

Side view and cross section of the turbulent puff studied in the present work, together with the reference coordinate axis. (Online version in colour.)

Figure 2.

Time history of the vertical displacement of the puff centre of mass. The red circles and blue squares represent the data from the case with low and high buoyancy. (Online version in colour.)

Figure 3.

Scaling laws for the bulk properties of the puff: $L$ (filled symbols), $u_L$ (empty symbols) and $T_L$ (half-filled symbols) (divided by a factor two for graphical reasons) for (a) shear-induced fluctuations and (b) buoyancy-driven fluctuations. The data reported in the left panel are taken from [8]. In the figures, the solid lines represent the proposed scaling laws, while the symbols the results of our simulations. (Online version in colour.)

Figure 4.

Scaling laws for the non-dimensional numbers of the puff: (a) $Re$ and (b) $Ra$ for shear-induced fluctuations (red circles) and buoyancy-driven fluctuations (blue squares). In the figures, the solid lines represent the proposed scaling laws, while the symbols the results of our simulations. (Online version in colour.)

Figure 5.

Second-order structure function for the (a,b) velocity and (c,d) temperature difference: (a,c) raw data and (b,d) data scaled by the predicted inertial scaling. In the figures, the solid lines represent the proposed scaling laws, while the symbols the results of our simulations. The data refer to the time interval $3\lesssim t/t_0\lesssim 10$, with colours indicating different time instants separated by an interval of $t_0$ in the following order: dark-blue, blue, grey, light-green, green and brown. (Online version in colour.)

Figure 6.

Time histories of (a,b) $S_2^{\parallel }(r)$ (filled symbols), $S_4^{\parallel }(r)$ (empty symbols) and $S_6^{\parallel }(r)$ (half-filled symbols) and of (c,d) $S_2(r)$ (filled symbols), $S_4(r)$ (empty symbols) and $S_6(r)$ (half-filled symbols) for two separations taken in the inertial (a,c) and viscous (b,d) range of scales, for the case with buoyancy-driven fluctuations. In the figures, the solid lines represent the proposed scaling laws, while the symbols the results of our simulations. (Online version in colour.)

Figure 7.

(a,b) (left) $S_4^{\parallel }(r)$ and (right) $S_6^{\parallel }(r)$ as a function of $S_2^{\parallel }(r)$ and (c,d) (left) $S_4(r)$ and (right) $S_6(r)$ as a function of $S_2(r)$. All the structure functions are divided by their expected temporal scalings. The symbols represent the data from the case with high buoyancy, while the solid and dotted lines represent the ratio of the expected spatial scaling laws with and without the intermittency corrections. (Online version in colour.)