Haplotype-based inference of the distribution of fitness effects
- PMID: 35100400
- PMCID: PMC8982047
- DOI: 10.1093/genetics/iyac002
Haplotype-based inference of the distribution of fitness effects
Abstract
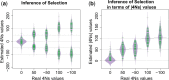
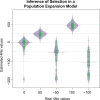
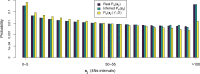
Recent genome sequencing studies with large sample sizes in humans have discovered a vast quantity of low-frequency variants, providing an important source of information to analyze how selection is acting on human genetic variation. In order to estimate the strength of natural selection acting on low-frequency variants, we have developed a likelihood-based method that uses the lengths of pairwise identity-by-state between haplotypes carrying low-frequency variants. We show that in some nonequilibrium populations (such as those that have had recent population expansions) it is possible to distinguish between positive or negative selection acting on a set of variants. With our new framework, one can infer a fixed selection intensity acting on a set of variants at a particular frequency, or a distribution of selection coefficients for standing variants and new mutations. We show an application of our method to the UK10K phased haplotype dataset of individuals.
Keywords: DFE; haplotype; inference; selection.
© The Author(s) 2022. Published by Oxford University Press on behalf of Genetics Society of America.
Figures


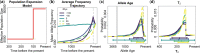



References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

