Multiple timescales in bacterial growth homeostasis
- PMID: 35118352
- PMCID: PMC8792075
- DOI: 10.1016/j.isci.2021.103678
Multiple timescales in bacterial growth homeostasis
Abstract
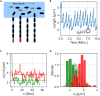
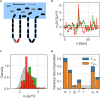
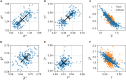
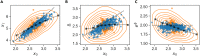
In balanced exponential growth, bacteria maintain many properties statistically stable for a long time: cell size, cell cycle time, and more. As these are strongly coupled variables, it is not a-priori obvious which are directly regulated and which are stabilized through interactions. Here, we address this problem by separating timescales in bacterial single-cell dynamics. Disentangling homeostatic set points from fluctuations around them reveals that some variables, such as growth-rate, cell size and cycle time, are "sloppy" with highly volatile set points. Quantifying the relative contribution of environmental and internal sources, we find that sloppiness is primarily driven by the environment. Other variables such as fold-change define "stiff" combinations of coupled variables with robust set points. These results are manifested geometrically as a control manifold in the space of variables: set points span a wide range of values within the manifold, whereas out-of-manifold deviations are constrained. Our work offers a generalizable data-driven approach for identifying control variables in a multidimensional system.
Keywords: Microbiology; Systems biology.
© 2021 The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures

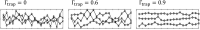




References
-
- Amir A. Cell size regulation in bacteria. Phys. Rev. Lett. 2014;112:208102.
-
- Braun E. Academic Press; 2020. Cell-state organization by exploratory sloppy dynamics. Phenotypic Switching; pp. 305–334.
-
- Brenner N., Braun E., Yoney A., Susman L., Rotella J., Salman H. Single-cell protein dynamics reproduce universal fluctuations in cell populations. Eur. Phys. J. E. 2015;38:102. - PubMed
-
- Brenner N., Newman C.M., Osmanović D., Rabin Y., Salman H., Stein D.L. Universal protein distributions in a model of cell growth and division. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 2015;92:042713. - PubMed
LinkOut - more resources
Full Text Sources
Molecular Biology Databases
Research Materials

