"De-Shrinking" EBEs: The Solution for Bayesian Therapeutic Drug Monitoring

Abstract

Background: Therapeutic drug monitoring (TDM) aims at individualising a dosage regimen and is increasingly being performed by estimating individual pharmacokinetic parameters via empirical Bayes estimates (EBEs). However, EBEs suffer from shrinkage that makes them biased. This bias is a weakness for TDM and probably a barrier to the acceptance of drug dosage adjustments by prescribers.

Objective: The aim of this article is to propose a methodology that allows a correction of EBE shrinkage and an improvement in their precision.

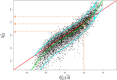
Methods: As EBEs are defined, they can be seen as a special case of ridge estimators depending on a parameter usually denoted λ. After a bias correction depending on λ, we chose λ so that the individual pharmacokinetic estimations have minimal imprecision. Our estimate is by construction always better than EBE with respect to bias (i.e. shrinkage) and precision.

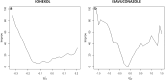
Results: We illustrate the performance of this approach with two different drugs: iohexol and isavuconazole. Depending on the patient's actual pharmacokinetic parameter values, the improvement given by our approach ranged from 0 to 100%.

Conclusion: This innovative methodology is promising since, to the best of our knowledge, no other individual shrinkage correction has been proposed.

Fig. 1

The y-axis represents the ${\eta }_{\text{Cl}}^{\ast }$ that have been used to simulate the concentrations; the x-axis contains the ${\widehat{\eta }}_{\text{Cl}}^{\ast }\left(\widehat{\lambda }\right)$ obtained from the procedure described in section 2.1. The red line is the first bisector line. For a patient P, having a clearance individual random effect, denoted by ${\eta }_{\text{Cl,P}}^{\ast }$, far below or above zero or, equivalently, an individual pharmacokinetic parameter far from the typical value, there is a systematic error. The systematic error is represented on the plot by the distance of the green curve from the red curve. The green curve represents ${\mathrm{\Gamma }}_{\widehat{\lambda }}\left({\widehat{\eta }}_{\text{Cl}}\left(\widehat{\lambda }\right)\right)$. The blue band is the 95% prediction interval. Its width, for a given ${\widehat{\eta }}_{\text{Cl,P}}\left(\widehat{\lambda }\right)$ (i.e., for a given patient) gives an evaluation of the imprecision of our method

Fig. 2

Graphical representation of ${\eta }_{\text{Cl}}^{\ast }$ as a function of ${\widehat{\eta }}_{\text{Cl}}^{\ast }\left(1\right)$ (i.e. empirical Bayes estimate for clearance) (left) and of ${\eta }_{\text{Cl}}^{\ast }$ as a function of ${\mathrm{\Gamma }}_{\widehat{\lambda }}\left({\widehat{\eta }}_{\text{Cl}}^{\ast }\left(\widehat{\lambda }\right)\right)$ (right). The red curves represent the first bisector, the green curve represents the regression line, and the blue curves represent the prediction interval. After correction, the point clouds are refocused on the first bisector

Fig. 3

Graphical representation of the evolution of “Improv” of iohexol and isavuconazole. Improvement is much more important for values far from the average than for values close to the mean. The improvement of the estimates following the correction of the empirical Bayes estimate is therefore not always the same. So, this methodology does not provide a great correction for patients who have a pharmacokinetic profile close to the average. However, for pharmacokinetic profiles far from average pharmacokinetic profiles (i.e. patients for whom therapeutic drug monitoring is usually indicated), this methodology greatly improves results