Predictive coding of natural images by V1 firing rates and rhythmic synchronization

Abstract

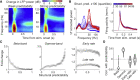
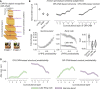
Predictive coding is an important candidate theory of self-supervised learning in the brain. Its central idea is that sensory responses result from comparisons between bottom-up inputs and contextual predictions, a process in which rates and synchronization may play distinct roles. We recorded from awake macaque V1 and developed a technique to quantify stimulus predictability for natural images based on self-supervised, generative neural networks. We find that neuronal firing rates were mainly modulated by the contextual predictability of higher-order image features, which correlated strongly with human perceptual similarity judgments. By contrast, V1 gamma (γ)-synchronization increased monotonically with the contextual predictability of low-level image features and emerged exclusively for larger stimuli. Consequently, γ-synchronization was induced by natural images that are highly compressible and low-dimensional. Natural stimuli with low predictability induced prominent, late-onset beta (β)-synchronization, likely reflecting cortical feedback. Our findings reveal distinct roles of synchronization and firing rates in the predictive coding of natural images.

Keywords: V1; beta oscillations; deep neural networks; gamma oscillations; gamma synchronization; predictive coding; primate; surround suppression.

Figure 1

Recording paradigm and machine learning method to compute predictability for natural scenes (A) Natural images were presented for 1.2 s (in a subset of sessions, for 0.6 s). (Left panel) Green dots indicate locations of RF centers of the recording array in monkey H. Image is cut out around the RF locations. (Center) Median example trace of the LFP for the image shown on the left. The 25–100 Hz filtered trace has arbitrary units. (Right) Example raster plot for MUA (spikes threshold at 3 s.d). (B) Illustration of a deep neural network (DNN) trained to predict visual inputs into the RFs. A mask of approximately the same size as the recording site’s RF is applied to an image. The image with the mask is then entered as an input to a DNN with a U-net architecture. This DNN generates (predicts) the full image, i.e., the image content behind the mask is filled in. Stimulus predictability is computed by comparing the ground-truth input image and the predicted image and then used for network optimization during the training stage. After network training, a novel set of images is presented to both the DNN and the monkeys. The predictability score is then correlated with LFP and spiking responses across images. See also Figure S1.

Figure 2

Distinct relationships of firing rates and neural synchronization with structural predictability (A) Average time-frequency representations for weak and strong structural predictability. (B) (Left) Average 1/f-corrected LFP power spectra for monkey H, for different levels of structural predictability. Black line indicates the pre-stimulus period. SEMs are shown only for the lowest and highest quantile of structural predictability. (Right) Multi-unit firing rates. (C) (Left) Average (±SEM) 1/f-corrected β-peak amplitude versus structural predictability. Average was computed across all recording sites in the three animals ($\text{n}=72$ sites). (Middle) Same for γ. (Right) Same for early (50–150 ms) and late firing rates (200–600 ms). (D) Pearson-r correlation across recording sites (with a minimum RMS contrast of 0.1) between structural predictability and γ, β, and rate. Correlations were computed for each recording site separately, using all images presented across sessions. Correlations were significant for β, γ, and early rates (all $\text{p}<0.001$) but not for late rates ($\text{p}=0.11$) (t test). Absolute correlations were higher for γ and β than early and late rates ($\text{p}<0.001$ for all comparisons). Data in (B and C) are represented as mean ± SEM. See also Figure S2.

Figure 3

Synchronization reflects image compressibility and dimensionality and distinguishes natural image categories (A) Two examples of images that have a low and high compression rate, structural predictability and γ values (as log₁₀-fold change), respectively. Compression rate was measured as the number of bits/pixel for image compression. (B) (Left) Compressibility (i.e., negative of compression rate) versus average structural predictability. (Right) Correlation between compressibility and structural predictability across images. (C) Average correlation (across recording sites) between compressibility and γ and firing intensity across images. (D) (Left) Images with low dimensionality had strong γ synchronization (r across quantiles = −0.9, $\text{p}<0.001$). Dimensionality was determined from the slope of the image spectrum. (Right) Average magnitude of spectral image components versus structural predictability (Pearson’s r = −0.91, $\text{p}<0.001$). (E) Fold-changes in neural activity for images with man-made content or nature content in the RF. Comparison was significant for β ($\text{p}<0.001$) and γ ($\text{p}<0.001$), but not for early and late rates ($\text{p}=0.5$ and $\text{p}=0.9$, t test). (Right) Percentage of sites with a detectable β or a γ peak, across all randomly selected images. Data in (B and D) (left) are represented as mean ± SEM. See also Figure S3.

Figure 4

Dependence of neural activity on luminance contrast and predictability (A) (Left) Average 1/f-corrected LFP power spectra (±1 SEM) for the highest and lowest level of luminance contrast (root means square contrast [RMS], see STAR Methods), for monkey H. (Right) As left, but for multi-unit firing rates. (B) (Left) Average γ-peak amplitude versus luminance contrast. (Right) Same for early (50–150 ms) and late MU firing rates (200–600 ms). (C) Average correlation across sites of γ and firing rate with image factors. Left-to-right: (Ci) Luminance contrast (Cntr); (Cii) the product of contrast and stimulus predictability (Cntr × Pred.); (Ciii) Pred, Cntr, Pred. × Cntr interaction (Full regression (regr.) model); and (Civ) a model with additional low-level features (Including (Incl.) other stim factors), namely spatial frequency, luminance and orientation (see STAR Methods). Correlations were computed for each recording site separately, across all images presented across sessions. All correlations were significantly different from zero ($\text{p}<0.001$, paired t test). For γ, the difference between (Cntr × Pred.) and (Full regr. model) was significant ($\text{p}<0.001$), but the difference between (Full regr. model) and (Incl. other stim factors) was not ($\text{p}>0.05$). For early rates, all comparisons were significant ($\text{p}<0.05$). For late rates, all comparisons except for (Full regr. model) versus (Cntr × Pred.) were significant at $\text{p}<0.05$. (D) γ fold-changes for different levels of luminance contrast and structural predictability. (E) Illustration of interaction between predictability and bottom-up inputs. (F) Derivation of the PUN measure (predictability under noise, left). We added Poisson noise to each luminance value and then computed the structural predictability for the noise-corrupted image, yielding the PUN measure. PUN was strongly correlated to the original luminance contrast in the center RF (right). (G) (Left) PUN correlated more strongly with γ synchronization than predictability and luminance contrast ($\text{p}<0.001$ for both, paired t test). (Right) For late firing rates, correlations with PUN were weaker than for luminance contrast ($\text{p}<0.001$). For a comparison of baseline-corrected γ-power with 1/f-corrected γ-power, an analysis of reliability of the predictors, and analysis of other stimulus factors, see Figure S4. Data in (A and B) are represented as mean ± SEM. See also Figure S4.

Figure 5

A feedforward neural network for object recognition explains firing rates relatively well, but poorly accounts for γ-synchronization (A) For each recording site, we determined different neural activity parameters. The image patch centered on the RF of the recording site was then passed into the CNN for object recognition (OR-CNN; in this case the VGG-16), and we computed the activation of every OR-CNN artificial neuron (AN) whose RF overlapped with the recording site. Sparse L1-regression with cross-validation was used to predict neural activity from OR-CNN ANs with RFs at the center of the image. (B) Regression prediction accuracy of different neural activity parameters depending on OR-CNN layer. Data are represented as mean ± SEM. Regression prediction accuracy for late (200–600 ms) firing rates was significantly higher for middle (5–9) than early (1–4) and deep (10–13) convolutional layers ($\text{p}<0.001$, paired t test). For γ, regression prediction accuracy was significantly higher for middle ($\text{p}<0.001$) and deep ($\text{p}<0.05$) than early layers. For early rates and β see Figures S5A and S5B. (C) Prediction accuracy depending on the RF location of OR-CNN ANs in the image. In this case, we predicted neural activity from all units in a 3 × 3 image using sparse L1-regression. Shown are the prediction weights, which reveal circular RFs for firing rates already in the earliest layer. See also Figure S5.

Figure 6

Firing rates reflect high-level stimulus predictability, gamma reflects low-level stimulus predictability (A) OR-CNN network (VGG-16) used to define low- and high-level stimulus similarity and predictability. Responses of artificial units (ANs) in different layers OR-CNN layers were computed for two images at a time. For each layer, we computed two similarity measures: (A1) content similarity, which is based on Euclidean distance; (A2) OR-CNN-based structural similarity, which was computed as the Pearson correlation across locations for each AN separately and then averaging these correlations across ANs. (B) (Left) Average AUC value for (B1) LPIPS, (B2) SSIM, (B3) structural correlations, as used for Figures 1 and 2. Learned perceptual image patch similarity (LPIPS) is a perceptual similarity measure based on OR-CNNs (Zhang et al., 2018). LPIPS had higher AUC values than the other measures ($\text{p}<0.001$, paired t test). (Right) Structural and content similarity versus human perceptual similarity. AUC increased significantly with layer depth for both structure and content (r = 0.93 and r = 0.98, $\text{p}<0.001$ for both). (C) (Left) Firing rates and neural synchronization versus LPIPS-predictability. The input (ground-truth) and predicted image-patch were compared using the OR-CNN network, yielding LPIPS-predictability. (Right) Correlations across all images, averaged across recording sites ($\text{p}<0.001)$ for all variables). (D) Correlation of late firing rates and peak γ-power with OR-CNN-based content and structural predictability across OR-CNN layers. See Figure S6C for example images with different levels of low- and high-level content predictability. Note that, we first computed average correlations and show here the absolute average value of these correlations, but that correlations were positive for γ and negative for firing rates. Late firing rates showed a significant increase in absolute correlation across OR-CNN layers, both for OR-CNN-based structural and content predictability (structure: $\text{r}=0.85$; content: $\text{r}=0.81$, $\text{p}<0.001$ for both). By contrast, γ showed a significant decrease for both (structure: $\text{r}=0.9$; content: $\text{r}=0.84$, $\text{p}<0.001$). The average correlation (across layers) for OR-CNN-based structural predictability was significantly higher than OR-CNN-based content predictability for γ ($\text{p}<0.001$, paired t test). For firing rates, the average correlation with OR-CNN-based content predictability was higher than for OR-CNN-based structural predictability ($\text{p}<0.001$, paired t test). Data in (B–D) are represented as mean ± SEM. See also Figure S6.

Figure 7

Firing rates and gamma show distinct modulations by spatial context (A) Center-surround mismatch paradigm with noise stimuli and center-only versus full stimuli. Stimuli had white, pink, or brown noise in the 1 dva center, and white, pink, or brown noise in the surround. Stimuli (6 dva) were centered on the recording site’s RF. Only recording sites within 0.25 dva of the stimuli center were analyzed. (Left) LFP power spectra. Note that the broadband increase in LFP power at high frequencies is typical for spike bleed-in Ray and Maunsell (2011). (Dashed line) Baseline pre-stimulus period. (Right) Normalized MU firing rates. Firing rates were higher for noise-mismatch stimuli (gray bar: $\text{p}<0.05$, t test, n = 24 recording sites). (B) (Left and right): Examples of surround suppression for image that show either clear gamma synchronization (left) or no clear peak in the gamma-range. (C) Comparison of gamma-amplitude and late firing rates for different stimulus sizes ($lo{g}_{10}$-fold-change for both). Suppression for early firing intensity was significantly weaker than for late firing intensity (paired t test, $\text{p}<0.001$). (D) Increase in γ-synchronization for full compared with small images as a function of structural predictability. (E) Surround modulation in firing rates (small minus full) as a function of structural predictability and LPIPS-predictability. Data in (A–C) are represented as mean ± SEM. See also Figure S7.