Statistical properties of sketching algorithms

Abstract

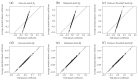
Sketching is a probabilistic data compression technique that has been largely developed by the computer science community. Numerical operations on big datasets can be intolerably slow; sketching algorithms address this issue by generating a smaller surrogate dataset. Typically, inference proceeds on the compressed dataset. Sketching algorithms generally use random projections to compress the original dataset, and this stochastic generation process makes them amenable to statistical analysis. We argue that the sketched data can be modelled as a random sample, thus placing this family of data compression methods firmly within an inferential framework. In particular, we focus on the Gaussian, Hadamard and Clarkson-Woodruff sketches and their use in single-pass sketching algorithms for linear regression with huge samples. We explore the statistical properties of sketched regression algorithms and derive new distributional results for a large class of sketching estimators. A key result is a conditional central limit theorem for data-oblivious sketches. An important finding is that the best choice of sketching algorithm in terms of mean squared error is related to the signal-to-noise ratio in the source dataset. Finally, we demonstrate the theory and the limits of its applicability on two datasets.

Keywords: Computational efficiency; Random projection; Randomized numerical linear algebra; Sketching.

Fig. 1

Bias of partial sketching estimators on the HLA dataset: panels (a)–(c) show results for β _P and panels (d)– (f) results for the bias-corrected estimator ${\beta }_{\text{P}}^{\ast }$ ; mean estimates are plotted against the true values. In this scenario n = 132 353, p = 1000 and k = 1500. The solid line in each panel is the identity line, and the dashed line in panels (a)–(c) represents the theoretical bias factor.