Species-range-size distributions: Integrating the effects of speciation, transformation, and extinction
- PMID: 35127000
- PMCID: PMC8796946
- DOI: 10.1002/ece3.8341
Species-range-size distributions: Integrating the effects of speciation, transformation, and extinction
Abstract
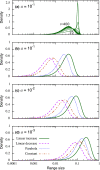
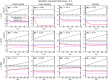
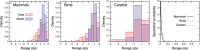
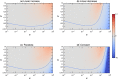
The species-range size distribution is a product of speciation, transformation of range-sizes, and extinction. Previous empirical studies showed that it has a left-skewed lognormal-like distribution. We developed a new mathematical framework to study species-range-size distributions, one in which allopatric speciation, transformation of range size, and the extinction process are explicitly integrated. The approach, which we call the gain-loss-allopatric speciation model, allows us to explore the effects of various speciation scenarios. Our model captures key dynamics thought to lead to known range-size distributions. We also fitted the model to empirical range-size distributions of birds, mammals, and beetles. Since geographic range dynamics are linked to speciation and extinction, our model provides predictions for the dynamics of species richness. When a species-range-size distribution initially evolves away from the range sizes at which the likelihood of speciation is low, it tends to cause diversification slowdown even in the absence of (bio)diversity dependence in speciation rate. Using the mathematical model developed here, we give a potential explanation for how observed range-size distributions emerge from range-size dynamics. Although the framework presented is minimalistic, it provides a starting point for examining hypotheses based on more complex mechanisms.
Keywords: diversification rate; geographic range‐size distribution; lineage‐through‐time plots; mathematical model.
© 2022 The Authors. Ecology and Evolution published by John Wiley & Sons Ltd.
Conflict of interest statement
The authors declare that they have no conflict of interest.
Figures


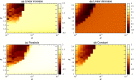
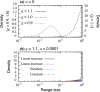
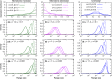
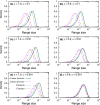





References
-
- Alzate, A. , Janzen, T. , Bonte, D. , Rosindell, J. , & Etienne, R. S. (2019). A simple spatially explicit neutral model explains the range size distribution of reef fishes. Global Ecology and Biogeography, 28, 875–890. 10.1111/geb.12899 - DOI
-
- Anderson, S. (1985). The theory of range‐size (RS) distributions. American Museum Novitates, 2833, 1–20.
-
- BirdLife International and Handbook of the Birds of the World . (2017). Bird species distribution maps of the world. Version 2017.2. Retrieved from http://datazone.birdlife.org/species/requestdis
LinkOut - more resources
Full Text Sources
Miscellaneous

