Molecular diameters of rarefied gases

Abstract

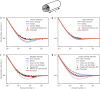
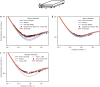
Molecular diameters are an important property of gases for numerous scientific and technical disciplines. Different measurement techniques for these diameters exist, each delivering a characteristic value. Their reliability in describing the flow of rarefied gases, however, has not yet been discussed, especially the case for the transitional range between continuum and ballistic flow. Here, we present a method to describe gas flows in straight channels with arbitrary cross sections for the whole Knudsen range by using a superposition model based on molecular diameters. This model allows us to determine a transition diameter from flow measurement data that paves the way for generalized calculations of gas behaviour under rarefied conditions linking continuum and free molecular regime.

Figure 1

Rarefied gas flow in technical applications and its dependence on the molecular diameter. (a) Typical Knudsen regions of technical applications. Materials for gas adsorption (cyan) can have pore sizes ranging over multiple orders of magnitude. In combination with large changes in pressure or temperature in swing-adsorption applications, the result is a wide Knudsen range. In catalysis (blue), products and educts often face small structures at high temperatures and Knudsen numbers larger than unity at atmospheric pressure can be observed. In space applications such as propulsion modules (magenta), the Knudsen numbers tend to be very large due to the low pressure in orbit. See Supplementary Text 1 for details on the Knudsen ranges. Left image: SEM image of a hierarchical structured zeolite adsorbent. Center image: SEM image of a Sm₂O₃ xerogel catalyst. Right image: Depiction of the ReFEx vehicle. (b) Schematic illustration of the individual transport terms of the superimposed model and their variation with the Knudsen number. The convective part decreases with rising Knudsen number while the diffusive part becomes dominant at Knudsen numbers larger than unity, because of the increasing mean free path. The diffusive part converges to a constant value at high Knudsen numbers where the surrounding geometry is the limiting factor for diffusion. The sum of both components reproduces the typical and well- known Knudsen minimum at approximately Kn = 1. The influence of the molecular diameter on the predicted mass flow is illustrated by the shaded areas.

Figure 2

Compilation of molecular diameters for small gases. (a) The van der Waals diameter^, has two definitions for an asymmetric molecule like carbon dioxide while a spherical gas like argon just has one. (b) Molecular sieve experiments yield the kinetic diameter. Molecular shape can have a large influence on the result. Here, carbon dioxide can pass the sieve in the right orientation, while argon is too large. This results in a larger kinetic diameter for argon than for carbon dioxide. (c) Viscosity (ν) can be measured by the momentum exchange from one moving boundary to a stationary one. The momentum exchanges through diffusion from fast moving molecules (top) to slow moving molecules (bottom). This diffusion is limited by the mean free path. While the two highlighted carbon dioxide molecules collide because of their size, the argon molecules can pass. The larger the molecules, the slower the molecules can diffuse, resulting in lower measured viscosity. This results in a larger viscous diameter for carbon dioxide than for argon. (d) Actual molecular sizes. Error bars show the two-sided prediction interval of 95%. The kinetic diameter of nitrogen and the diameter calculated from viscosity are covered by the transition diameter. The two van der Waals diameters for nitrogen and carbon dioxide are the transversal and the longitudinal ones. For numerical values, see Supplementary Table S1.

Figure 3

Mass flow in circular channels modelled with different molecular diameters compared to experimental data obtained from the literature. Dimensionless mass flow of helium (a), argon (b), nitrogen^, (c) and carbon dioxide (d) predicted by the model. The transition diameter is determined by least squares fitting to Eqs. (2)–(6). For comparison, the results for calculations using established molecular diameters from the literature are shown. For the nonspherical molecules nitrogen and carbon dioxide, two different van der Waals diameters are given for the transversal and longitudinal orientation, respectively.

Figure 4

Mass flow in rectangular channels modelled with different molecular diameters compared to experimental data obtained from the literature. Dimensionless mass flow of helium (a), argon (b) and nitrogen (c) predicted by the model. The transition diameters are obtained from data on circular channels. For comparison, the results for different typical literature diameters are shown. For the nonspherical molecule nitrogen, two different van der Waals diameters are given for the transversal and longitudinal orientation, respectively.

Figure 5

Deviation of modelled mass flow from experimental data for circular channels. The deviation is scattered without any discernible pattern, except for carbon dioxide, a strong indicator that the proposed model explains the experimental data well.

Figure 6

Deviation of modelled mass flow from experimental data for rectangular channels. The deviation shows some pattern that is strongly correlated to the pressure sensors used in different Kn regions.