Evolution of cooperation with contextualized behavior

Abstract

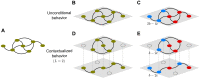
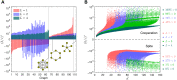
How do networks of social interaction govern the emergence and stability of prosocial behavior? Theoretical studies of this question typically assume unconditional behavior, meaning that an individual either cooperates with all opponents or defects against all opponents-an assumption that produces a pessimistic outlook for the evolution of cooperation, especially in highly connected populations. Although these models may be appropriate for simple organisms, humans have sophisticated cognitive abilities that allow them to distinguish between opponents and social contexts, so they can condition their behavior on the identity of opponents. Here, we study the evolution of cooperation when behavior is conditioned by social context, but behaviors can spill over between contexts. Our mathematical analysis shows that contextualized behavior rescues cooperation across a broad range of population structures, even when the number of social contexts is small. Increasing the number of social contexts further promotes cooperation by orders of magnitude.

Fig. 1.. Behavioral evolution with multiple social contexts.

(A) A population is described by a network with N nodes and E edges of weight 1. In a single social context, every individual takes the same action, namely, cooperation (blue; pay a cost c to bring the opponent a benefit b) or defection (red; pay no cost and bring no benefit), with each neighbor. (B and C) The total payoff of individual i, u_i, is accumulated across all interactions. We introduce multiple contexts by decomposing the network into L different layers (L = 2 depicted here), which represent different social contexts. (D) Nodes and edges are distributed among the L layers, with each edge occurring in one layer and each node occurring in one or more layers. Nodes connected via a dashed line between layers refer to the same individual who operates in multiple social contexts. (E) Each individual, i, uses (possibly) different behaviors in different contexts, plays a game with each neighbor in the same context, and obtains a payoff u_i^[1] in layer 1 and u_i^[2] in layer 2. Individual i’s accumulated payoff is summed over contexts u_i = u_i^[1] + u_i^[2]. Increasing the number of layers L means allowing a greater number of contexts on which individuals may condition their behavior.

Fig. 2.. Why contextualized behavior can favor cooperation.

A cooperator i (blue circle) and a defector j (red circle) compete to disperse their behavior to the vacancy (white circle). Because an individual spreads behaviors only in her neighborhood, the probability that one of i’s neighbors (olive blue circle) is a cooperator, P_C∣C, exceeds that of j’s neighbors (olive red circle), P_C∣D. (A) In a single social context, compared with the defector j, the cooperator i receives b(P_C∣C − P_C∣D) more benefit from each neighbor; at the same time, she pays a cost c in each interaction, leading to a payoff difference of b(P_C∣C − P_C∣D) − c per interaction. (B) With multiple social contexts, compared with a defector at j^[1] in layer 1, a cooperator at i^[1] receives b(P_C∣C − P_C∣D) more benefit, and she also pays a cost c in each interaction. Because of strategy spillover between layers, the probability that i’s neighbor in layer 2 is a cooperator (say P_C∣C) is larger than j’s neighbor in layer 2 (say P_C∣D). Therefore, compared with j^[2], i^[2] receives b(P_C∣C − P_C∣D) more benefit from each neighbor in layer 2. But i is not required to be a cooperator in layer 2, nor is j required to be a defector in layer 2. Overall, the cooperator at i^[1] effectively acquires an extra benefit of b(P_C∣C − P_C∣D) from each interaction in layer 2 while reducing the cost of cooperation.

Fig. 3.. Evolution of cooperation with contextualized behavior.

(A) There are 112 connected graphs of size N = 6. In a single social context (L = 1; red bars), 65 such graphs favor the evolution of spite [(b/c)* < 0], 42 graphs favor the evolution of cooperation for sufficiently large benefit-to-cost ratio [(b/c)* > 0], and 5 graphs never favor cooperation [(b/c)* = ∞]. To study multiple social contexts, we randomly and uniformly distribute all edges over L layers, apportioning a fraction of 1/L of edges to each layer. For each graph, we sample 1000 such L-layer configurations and record the critical benefit-to-cost ratio (b/c)* that supports cooperation for each of them. The blue bars represent the average value of (b/c)* for L = 2 contexts. [Note that (b/c)* is averaged over ratios of the same sign.] Similarly, the teal bars represent the average value of (b/c)* for L = 4 contexts, where cooperation is always favored for some positive ratio (b/c)*. In (B), we analyze six classes of networks: random regular networks (RR), Erdös-Rényi networks (ER) (63), Watts-Strogatz small-world networks (SW) with rewiring probability 0.1 (64), Barabási-Albert scale-free networks (BA-SF) (65), Goh-Kahng-Kim scale-free networks (GKK-SF) (66) with γ = 2.5, and Holme-Kim scale-free networks (HK-SF) (67) with triad formation probability 0.1. For each of these classes, we investigate 50,000 networks of size N, where N is chosen uniformly from [80,160], and of average node degree $\overline{d}$, chosen uniformly from [4, N − 1]. For each network, we randomly and uniformly distribute the edges over L layers once and record the corresponding critical ratio. The proportion of population structures in which cooperation can evolve is monotonically increasing with L, rising from 45% when L = 1, to 73% when L = 2, to 99% when L = 3, and to 100% with L = 4 contexts.

Fig. 4.. Critical ratios and fixation probabilities on random regular graphs.

We consider a population of size N = 1000 described by a random regular network with node degree d. Contextual behavior is modeled by an L-layer network in which each layer is (d/L)-regular. (A) Each dot corresponds to the average over 100 L-layer networks, calculated exactly. Dashed lines indicate the rule of b/c > 2d/(L + 1), which is a reasonably good (but not perfect) fit. Qualitatively, we see that (b/c)* is a monotonically decreasing function of the number of social contexts, L. (B) Dots represent exact fixation probability ρ_C from Eq. 6, in a population of degree d = 30, selection strength δ = 0.01, and cost c = 1. Each dot corresponds to the average over 100 L-layer networks. Dashed lines mark the approximation with ${\tilde{\mathrm{\rho }}}_{\mathrm{C}}=(L+1)/4$, which, again, matches the exact value of ρ_C reasonably well. Qualitatively, this fixation probability of cooperators is a monotonically increasing function of the number of social contexts, L.