Intertwined spin, charge, and pair correlations in the two-dimensional Hubbard model in the thermodynamic limit

Abstract

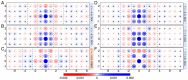
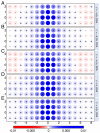
The high-temperature superconducting cuprates are governed by intertwined spin, charge, and superconducting orders. While various state-of-the-art numerical methods have demonstrated that these phases also manifest themselves in doped Hubbard models, they differ on which is the actual ground state. Finite-cluster methods typically indicate that stripe order dominates, while embedded quantum-cluster methods, which access the thermodynamic limit by treating long-range correlations with a dynamical mean field, conclude that superconductivity does. Here, we report the observation of fluctuating spin and charge stripes in the doped single-band Hubbard model using a quantum Monte Carlo dynamical cluster approximation (DCA) method. By resolving both the fluctuating spin and charge orders using DCA, we demonstrate that they survive in the doped Hubbard model in the thermodynamic limit. This discovery also provides an opportunity to study the influence of fluctuating stripe correlations on the model's pairing correlations within a unified numerical framework. Using this approach, we also find evidence for pair-density-wave correlations whose strength is correlated with that of the stripes.

Keywords: Hubbard model; dynamical cluster approximation; stripe.

Fig. 1.

The real-space static staggered spin–spin correlation function of the single-band Hubbard model with $\langle n\rangle =0.8$, obtained from DCA and DQMC simulations. Results are shown for $t\prime =-0.3t$, DCA (A); $t\prime =-0.25t$, DCA (B); $t\prime =-0.25t$, DQMC (C); $t\prime =-0.2t$, DCA (D); $t\prime =0$, DCA (E); and $t\prime =0.2t$, DCA (F). The DCA results were obtained by using a 16 × 4 cluster embedded in a dynamical mean field and at an inverse temperature $\beta =6/t$ (A, B, and D–F). The DQMC results shown in C were obtained on a $16\times 4$ cluster with periodic boundary conditions and $\beta =4.5/t$ and $t\prime =-0.25t$. Note that here and throughout, we have adopted the same custom color bars used in refs. 8 and 9. This scale provides a finer gradation of small values of the correlation function and improves the overall contrast (SI Appendix).

Fig. 2.

The real-space static density-density correlation function of the single-band Hubbard model, obtained from DCA and DQMC simulations. Results are shown for $t\prime =-0.3t$, DCA (A); $t\prime =-0.25t$, DCA (B); $t\prime =-0.25t$, DQMC (C); $t\prime =-0.2t$, DCA (D); $t^{\prime }=0$, DCA (E); and $t\prime =0.2t$, DCA (F). The DCA results were obtained by using a $16\times 4$ cluster embedded in a dynamical mean field and at an inverse temperature $\beta =6/t$ (A, B, and D–F). The DQMC results shown in C were obtained on a 16 × 4 cluster with periodic boundary conditions and $\beta =4.5/t$ and $t\prime =-0.25t$.

Fig. 3.

DCA results for the static spin $S(\mathbf{Q},\omega =0)$ (A–E) and charge $N(\mathbf{Q},\omega =0)$ (F–J) susceptibilities, obtained on a 16 × 4 cluster embedded in a dynamical mean field and with $\langle n\rangle =0.8$. A–E show the spin susceptibilities along $\mathbf{Q}=(Q_x,\pi )$ for $t\prime =-0.3t$ (A), $t\prime =-0.25t$ (B), $t\prime =-0.2t$ (C), $t\prime =0$ (D), and $t\prime =0.2t$ (E). Each curve is fit with a pair of Lorentzian functions centered at $(2\pi /a)(0.5\pm {\delta }_s,0.5)$ plus a constant background. F–J show the corresponding charge susceptibilities along $\mathbf{Q}=(Q_x,0)$. Each curve is fit with a pair of Lorentzian functions centered at $(2\pi /a)(\pm {\delta }_c,0)$ plus a constant background. All results were obtained for $T=0.167t$ ($\beta =6/t$). The ratio of the spin and charge incommensurabilities is given by $r={\delta }_s/{\delta }_c$, and K shows the temperature evolution of the spin and charge incommensurabilities and their ratio r for $t\prime =-0.3t$. L and M show the temperature dependence of the spin and charge correlation lengths, respectively, for the same $t\prime$.

Fig. 4.

The real-space static d-wave pairfield correlation function of the single-band Hubbard model. DCA results are shown for $t\prime =-0.3t$ (A), $-0.25t$ (B), $-0.2t$ (C), 0 (D), and $0.2t$ (E). The remaining model parameters are identical to those used in Fig. 1.

Fig. 5.

DCA results for the static pairfield susceptibility $P_d(\mathbf{Q},\omega =0)$ for $\langle n\rangle =0.8$ and $T=0.167t$ ($\beta =6/t$) obtained on a 16 × 4 cluster embedded in a dynamical mean field for $t\prime =-0.3t$ (A), $t\prime =-0.25t$ (B), $t\prime =-0.2t$ (C), $t\prime =0$ (D), and $t\prime =0.2t$ (E). Each curve is fit with a pair of Lorentzian functions centered at $(\pm {\delta }_P,0)$. For $t\prime =0.2t$, the two Lorentzians collapse onto a single peak centered at (0, 0).