Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Jun;477(2250):20210154.
doi: 10.1098/rspa.2021.0154. Epub 2021 Jun 2.

The reflection of a blast wave by a very intense explosion

Andrew W Cook  1 , Joseph D Bauer  1 , Gregory D Spriggs  1
Affiliations

The reflection of a blast wave by a very intense explosion

Andrew W Cook et al. Proc Math Phys Eng Sci. 2021 Jun.

Abstract

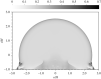
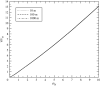
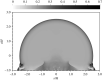
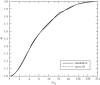
We demonstrate that the geometric similarity of Taylor's blast wave persists beyond reflection from an ideal surface. Upon impacting the surface, the spherical symmetry of the blast wave is lost but its cylindrical symmetry endures. As the flow acquires dependence on a second spatial dimension, an analytic solution of the Euler equations becomes elusive. However, the preservation of axisymmetry, geometric similarity and planar symmetry in the presence of a mirror-like surface causes all flow solutions to collapse when scaled by the height of burst (HOB) and the shock arrival time at the surface. The scaled blast volume for any yield, HOB and ambient air density follows a single universal trajectory for all scaled time, both before and after reflection.

Keywords: Taylor’s Equation; airdrops; blast waves; nuclear detonations; numerical simulations; surface detonations.

PubMed Disclaimer

Figures

Figure 1.
Figure 1.
The Mohawk event at t = 0.010148 s. The bulbous jet on the right was caused by shielding placed alongside the device.
Figure 2.
Figure 2.
Blast volume versus time for a 100 kt detonation at 100 m HOB in a 1 kg m−3 density atmosphere.
Figure 3.
Figure 3.
Non-dimensional pressure at t/tH = 10 for a 100 kt detonation at 10 m HOB (left) versus 1 km HOB (right).
Figure 4.
Figure 4.
Non-dimensional volume versus non-dimensional time for a 100 kt detonation at 10, 100 and 1000 m HOB.
Figure 5.
Figure 5.
Non-dimensional pressure at t/tH = 10 for a 10 kt detonation (left) versus a 1 Mt detonation (right) at 100 m HOB.
Figure 6.
Figure 6.
Non-dimensional volume versus non-dimensional time for 10 kt, 100 kt and 1 Mt detonations at 100 m HOB.
Figure 7.
Figure 7.
Non-dimensional pressure at t/tH = 10 for a 100 kt detonation at 100 m HOB with ambient density 0.1 kg m−3 (left) versus 10 kg m−3 (right).
Figure 8.
Figure 8.
Non-dimensional volume versus non-dimensional time for a 100 kt detonation at 100 m HOB with ambient densities 0.1 kg m−3, 1 kg m−3 and 10 kg m−3.
Figure 9.
Figure 9.
The reflection function (4.2) for all simulations.
See this image and copyright information in PMC

References

    1. Taylor GI. 1950. The formation of a blast wave by a very intense explosion I. Theoretical discussion. Proc. R. Soc. Lond. A 201, 159–174. (10.1098/rspa.1950.0049) - DOI
    1. Taylor GI. 1950. The formation of a blast wave by a very intense explosion. II. The atomic explosion of 1945. Proc. R. Soc. Lond. A 201, 175–187. (10.1098/rspa.1950.0050) - DOI
    1. von Neumann J, Richtmyer RD. 1950. A method for the numerical calculations of hydrodynamical shocks. J. Appl. Phys. 21, 232–237. (10.1063/1.1699639) - DOI
    1. Sedov LI. 1959. Similarity and dimensional methods in mechanics, 4th edn. New York, NY: Academic Press.
    1. Tang S, Wang QD. 2005. Supernova blast waves in low-density hot media: A mechanism for spatially distributed heating. Astrophys. J. 628, 205–209. (10.1086/430875) - DOI