Bayesian mechanics for stationary processes
- PMID: 35153603
- PMCID: PMC8652275
- DOI: 10.1098/rspa.2021.0518
Bayesian mechanics for stationary processes
Abstract
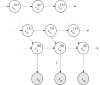
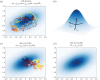
This paper develops a Bayesian mechanics for adaptive systems. Firstly, we model the interface between a system and its environment with a Markov blanket. This affords conditions under which states internal to the blanket encode information about external states. Second, we introduce dynamics and represent adaptive systems as Markov blankets at steady state. This allows us to identify a wide class of systems whose internal states appear to infer external states, consistent with variational inference in Bayesian statistics and theoretical neuroscience. Finally, we partition the blanket into sensory and active states. It follows that active states can be seen as performing active inference and well-known forms of stochastic control (such as PID control), which are prominent formulations of adaptive behaviour in theoretical biology and engineering.
Keywords: Markov blanket; active inference; free-energy principle; non-equilibrium steady state; predictive processing; variational Bayesian inference.
© 2021 The Authors.
Figures

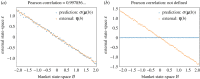
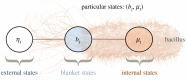
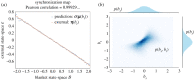
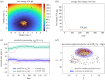
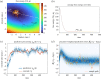
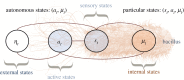
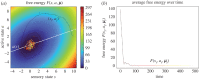
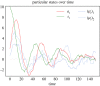
Similar articles
-
Markov blankets, information geometry and stochastic thermodynamics.Philos Trans A Math Phys Eng Sci. 2020 Feb 7;378(2164):20190159. doi: 10.1098/rsta.2019.0159. Epub 2019 Dec 23. Philos Trans A Math Phys Eng Sci. 2020. PMID: 31865883 Free PMC article.
-
Stochastic Chaos and Markov Blankets.Entropy (Basel). 2021 Sep 17;23(9):1220. doi: 10.3390/e23091220. Entropy (Basel). 2021. PMID: 34573845 Free PMC article.
-
Future climates: Markov blankets and active inference in the biosphere.J R Soc Interface. 2020 Nov;17(172):20200503. doi: 10.1098/rsif.2020.0503. Epub 2020 Nov 25. J R Soc Interface. 2020. PMID: 33234063 Free PMC article.
-
Neural and phenotypic representation under the free-energy principle.Neurosci Biobehav Rev. 2021 Jan;120:109-122. doi: 10.1016/j.neubiorev.2020.11.024. Epub 2020 Nov 30. Neurosci Biobehav Rev. 2021. PMID: 33271162 Free PMC article. Review.
-
Path integrals, particular kinds, and strange things.Phys Life Rev. 2023 Dec;47:35-62. doi: 10.1016/j.plrev.2023.08.016. Epub 2023 Aug 29. Phys Life Rev. 2023. PMID: 37703703 Review.
Cited by
-
Forced Friends: Why the Free Energy Principle Is Not the New Hamilton's Principle.Entropy (Basel). 2024 Sep 18;26(9):797. doi: 10.3390/e26090797. Entropy (Basel). 2024. PMID: 39330130 Free PMC article. Review.
-
Epistemic Communities under Active Inference.Entropy (Basel). 2022 Mar 29;24(4):476. doi: 10.3390/e24040476. Entropy (Basel). 2022. PMID: 35455140 Free PMC article.
-
Analyzing asymmetry in brain hierarchies with a linear state-space model of resting-state fMRI data.Netw Neurosci. 2024 Oct 1;8(3):965-988. doi: 10.1162/netn_a_00381. eCollection 2024. Netw Neurosci. 2024. PMID: 39355437 Free PMC article.
-
A Variational Synthesis of Evolutionary and Developmental Dynamics.Entropy (Basel). 2023 Jun 21;25(7):964. doi: 10.3390/e25070964. Entropy (Basel). 2023. PMID: 37509911 Free PMC article.
-
Memory and Markov Blankets.Entropy (Basel). 2021 Aug 25;23(9):1105. doi: 10.3390/e23091105. Entropy (Basel). 2021. PMID: 34573730 Free PMC article.
References
-
- Hesp C, Ramstead M, Constant A, Badcock P, Kirchhoff M, Friston K. 2019. A multi-scale view of the emergent complexity of life: a free-energy proposal. In Evolution, development and complexity (eds GY Georgiev, JM Smart, CL Flores Martinez, ME Price). Springer Proceedings in Complexity, pp. 195–227, Cham: Springer International Publishing.
-
- Pearl J. 1998. Graphical models for probabilistic and causal reasoning. In Quantified representation of uncertainty and imprecision (ed. P Smets). Handbook of Defeasible Reasoning and Uncertainty Management Systems, pp. 367–389. Netherlands, Dordrecht: Springer.
-
- Bishop CM. 2006. Pattern recognition and machine learning. Information Science and Statistics. New York, NY: Springer.
-
- Nicolis G, Prigogine I. 1977. Self-organization in nonequilibrium systems: from dissipative structures to order through fluctuations. New York, NY: Wiley-Blackwell.
Grants and funding
LinkOut - more resources
Full Text Sources

