Bayesian mechanics for stationary processes
- PMID: 35153603
- PMCID: PMC8652275
- DOI: 10.1098/rspa.2021.0518
Bayesian mechanics for stationary processes
Abstract
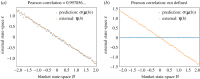
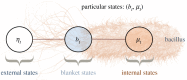
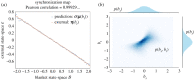
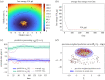
This paper develops a Bayesian mechanics for adaptive systems. Firstly, we model the interface between a system and its environment with a Markov blanket. This affords conditions under which states internal to the blanket encode information about external states. Second, we introduce dynamics and represent adaptive systems as Markov blankets at steady state. This allows us to identify a wide class of systems whose internal states appear to infer external states, consistent with variational inference in Bayesian statistics and theoretical neuroscience. Finally, we partition the blanket into sensory and active states. It follows that active states can be seen as performing active inference and well-known forms of stochastic control (such as PID control), which are prominent formulations of adaptive behaviour in theoretical biology and engineering.
Keywords: Markov blanket; active inference; free-energy principle; non-equilibrium steady state; predictive processing; variational Bayesian inference.
© 2021 The Authors.
Figures

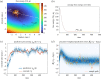
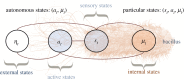
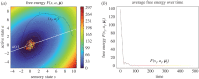
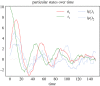
References
-
- Hesp C, Ramstead M, Constant A, Badcock P, Kirchhoff M, Friston K. 2019. A multi-scale view of the emergent complexity of life: a free-energy proposal. In Evolution, development and complexity (eds GY Georgiev, JM Smart, CL Flores Martinez, ME Price). Springer Proceedings in Complexity, pp. 195–227, Cham: Springer International Publishing.
-
- Pearl J. 1998. Graphical models for probabilistic and causal reasoning. In Quantified representation of uncertainty and imprecision (ed. P Smets). Handbook of Defeasible Reasoning and Uncertainty Management Systems, pp. 367–389. Netherlands, Dordrecht: Springer.
-
- Bishop CM. 2006. Pattern recognition and machine learning. Information Science and Statistics. New York, NY: Springer.
-
- Nicolis G, Prigogine I. 1977. Self-organization in nonequilibrium systems: from dissipative structures to order through fluctuations. New York, NY: Wiley-Blackwell.
Grants and funding
LinkOut - more resources
Full Text Sources
