Coarse Grained Modeling of Multiphase Flows with Surfactants

Abstract

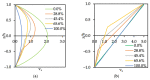
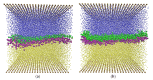
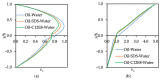
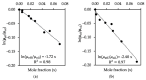
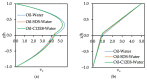
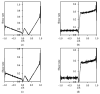
Coarse-grained modeling methods allow simulations at larger scales than molecular dynamics, making it feasible to simulate multifluid systems. It is, however, critical to use model parameters that represent the fluid properties with fidelity under both equilibrium and dynamic conditions. In this work, dissipative particle dynamics (DPD) methods were used to simulate the flow of oil and water in a narrow slit under Poiseuille and Couette flow conditions. Large surfactant molecules were also included in the computations. A systematic methodology is presented to determine the DPD parameters necessary for ensuring that the boundary conditions were obeyed, that the oil and water viscosities were represented correctly, and that the velocity profile for the multifluid system agreed with the theoretical expectations. Surfactant molecules were introduced at the oil-water interface (sodium dodecylsulfate and octaethylene glycol monododecyl ether) to determine the effects of surface-active molecules on the two-phase flow. A critical shear rate was found for Poiseuille flow, beyond which the surfactants desorbed to form the interface forming micelles and destabilize the interface, and the surfactant-covered interface remained stable under Couette flow even at high shear rates.

Keywords: coarse grained computations; multiphase flow; oil–water interfaces; surfactants.

Figure 1

Flow of two immiscible fluids between a pair of plates under (a) Poiseuille, and (b) Couette flow conditions.

Figure 2

Schematic configuration of heptadecane, water, SDS, and C12E8 surfactant molecules as beads of the DPD simulations. Hydrogen, carbon, oxygen, and sulfur molecules are shown as white, gray, red, and yellow spheres, respectively. The circles represent the DPD beads that group atoms or molecules together.

Figure 3

Poiseuille flow velocity profile for water with different dissipative parameter values between the wall and the water beads.

Figure 4

(a) Relation between the dissipative parameter and computed fluid viscosity, and (b) Poiseuille flow velocity profile for oil flow when ${\gamma }_{oil-oil}=22.5$ and ${\gamma }_{oil-wall}=45.0$.

Figure 5

Velocity profile for two immiscible fluids with various percentages of oil (0.0%, 28.8%, 48.4%, 65.6%, and 100.0%) under (a) Poiseuille and (b) Couette flow conditions. The oil flows through the bottom side of the channel and the water through the top side of the channel.

Figure 6

Snapshots of (a) SDS and (b) C12E8 surfactant at the oil–water interface with 50% of oil and water between two solid walls under Poiseuille flow. The wall, water, and oil beads are shown as ochre, blue, and yellow, respectively. The surfactant tails are purple, while green beads represent the head beads of the surfactants.

Figure 7

Velocity profile of oil–SDS–water and oil–C12E8-water in (a) Poiseuille and (b) Couette flows. The oil flows in the bottom side of the channel (z/h < 0) and the water flows through the top side (z/h > 0). The results are for a computational box with a size of 20$\times 20\times 21 r_c^3$.

Figure 8

$\ln \left({\mu }_{eff}/{\mu }_{oil}\right)$ as a function of mole fraction $x_i$ of (a) SDS and (b) C12E8 used to stabilize the oil–water interface in the case of the oil phase and $\ln \left({\mu }_{eff}/{\mu }_{water}\right)$ as a function of mole fraction $x_i$ of (c) SDS and (d) C12E8 in the case of the water phase.

Figure 8

$\ln \left({\mu }_{eff}/{\mu }_{oil}\right)$ as a function of mole fraction $x_i$ of (a) SDS and (b) C12E8 used to stabilize the oil–water interface in the case of the oil phase and $\ln \left({\mu }_{eff}/{\mu }_{water}\right)$ as a function of mole fraction $x_i$ of (c) SDS and (d) C12E8 in the case of the water phase.

Figure 9

Shear rate and fluid behavior of Poiseuille flow for (a,e) oil–SDS–water and (c,f) oil–C12E8–water, and Couette flow for (b) oil–SDS–water and (d) oil–C12E8–water (box size 20$\times 20\times 21 r_c^3$). Oil flows through the bottom of the channel and water through the top side of the channel (a–d). The color code for the DPD beads in (e,f) follows the colors in Figure 6.

Figure 10

Fluid behavior of Poiseuille flow for (a) oil–SDS–water ($C_{SDS}=$ 50.3% CMC; $g_x$ = 0.09) and (b) oil–C12E8–water ($C_{C12E8}=$ 55.1% CMC; $g_x$ = 0.17). The color code for the DPD beads follows the colors in Figure 6. Water and oil beads have been hidden. Note the high local concentration of the surfactants in the circled areas. The contour plots of the density of SDS surfactant and C12E8 surfactant are presented in (c,d) to show the local increase in surfactant concentration along the interface.

Figure 11

Velocity profile of the SDS or C12E8 surfactant at the interface of oil–water flow with a computational box size of $20\times 20\times 51 r_c^3$ under (a) Poiseuille flow and (b) Couette flow configurations.

Figure 12

Shear rate and fluid behavior of Poiseuille flow for (a) oil–SDS–water and (c) oil–C12E8–water, and Couette flow for (b) oil–SDS–water and (d) oil–C12E8–water (box size: $20\times 20\times 51 r_c^3$). Oil flows through the left side of the channel and water through the right side of the channel. The inset is a density plot with the y-axis as the density of the oil–surfactant–water system.