Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Feb 4;15(3):1198.
doi: 10.3390/ma15031198.

Unveiling the Hidden Entropy in ZnFe2O4

Miguel Angel Cobos  1 , Antonio Hernando  1   2   3   4 , José Francisco Marco  5 , Inés Puente-Orench  6   7 , José Antonio Jiménez  8 , Irene Llorente  8 , Asunción García-Escorial  8 , Patricia de la Presa  1   9
Affiliations

Unveiling the Hidden Entropy in ZnFe2O4

Miguel Angel Cobos et al. Materials (Basel). .

Abstract

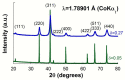
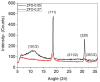
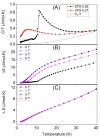
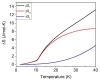
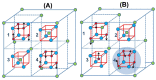
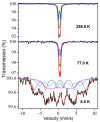
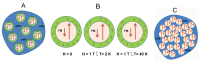
The antiferromagnetic (AFM) transition of the normal ZnFe2O4 has been intensively investigated with results showing a lack of long-range order, spin frustrations, and a "hidden" entropy in the calorimetric properties for inversion degrees δ ≈ 0 or δ = 0. As δ drastically impacts the magnetic properties, it is logical to question how a δ value slightly different from zero can affect the magnetic properties. In this work, (Zn1-δFeδ)[ZnδFe2-δ]O4 with δ = 0.05 and δ = 0.27 have been investigated with calorimetry at different applied fields. It is shown that a δ value as small as 0.05 may affect 40% of the unit cells, which become locally ferrimagnetic (FiM) and coexists with AFM and spin disordered regions. The spin disorder disappears under an applied field of 1 T. Mossbauer spectroscopy confirms the presence of a volume fraction with a low hyperfine field that can be ascribed to these spin disordered regions. The volume fractions of the three magnetic phases estimated from entropy and hyperfine measurements are roughly coincident and correspond to approximately 1/3 for each of them. The "hidden" entropy is the zero point entropy different from 0. Consequently, the so-called "hidden" entropy can be ascribed to the frustrations of the spins at the interphase between the AFM-FiM phases due to having δ ≈ 0 instead of ideal δ = 0.

Keywords: calorimetry; hidden entropy; neutron diffraction; spin disorder; zinc ferrite.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Figures

Figure 1
Figure 1
Diffraction patterns recorded at room temperature for the sample with δ = 0.27 and δ = 0.05.
Figure 2
Figure 2
NPD patterns for samples with δ = 0.05 and δ = 0.27.
Figure 3
Figure 3
(A) C/T for sample ZFO-0.05 (black line), ZFO-0.27 (red line), and lattice contribution CL/T (continuous line); (B) Entropy increase at different applied magnetic fields for ZFO-0.05; (C) for ZFO-0.27.
Figure 4
Figure 4
ΔS for sample with δ = 0.05, where the magnétic (red line), vibrational (blue line) and total entropy (black line) at H = 0 are shown separately.
Figure 5
Figure 5
(A) Half-cells of ZnFe2O4 with δ = 0, Fe3+ (red circles), and Zn2+ (green circles) in their corresponding octahedral (cells 1, 4) and tetrahedral (cells 2, 3) sites. Blue circles are oxygen. The black arrows indicate the magnetic moments. (B) A pair of Zn-Fe cations interchanged their sites; the stronger AFM A-B super exchange interaction leads to an FM order in the B sites and promotes some kind of frustration in the first neighbor’s B sites (shadow circle).
Figure 6
Figure 6
Entropy increment of ZFO-0.05 without applied field lifts up at 10 K regarding the curve at 1 T at the same temperature.
Figure 7
Figure 7
Calculated entropy increase for the paramagnetic region under a magnetic field of 0 T (black line), 1 T (blue line), and 9 T (red line).
Figure 8
Figure 8
Mossbauer spectra recorded at different temperatures from δ = 0.05.
Figure 9
Figure 9
(A) Illustration of magnetic arrangement of ZFO-0.05 sample, white circles representing ferrimagnetic particles, the blue area is AFM converted to PM at 40 K, and the green crown represents the disordered interphase between AFM and FM regions; (B) Different orientation of interphase area depending on the applied field (0, 1 T), and temperature; (C) Magnetic arrangement of ZFO-0.27 with percolating FM clusters and blue AFM regions.
See this image and copyright information in PMC

References

    1. Dolcet P., Kirchberg K., Antonello A., Suchomski C., Marschall R., Diodati S., Munoz-Espi R., Landfester K., Gross S. Exploring wet chemistry approaches to ZnFe2O4 spinel ferrite nanoparticles with different inversion degrees: A comparative study. Inorg. Chem. Front. 2019;6:1527–1534. doi: 10.1039/C9QI00241C. - DOI
    1. Bohra M., Alman V., Arras R. Nanostructured ZnFe2O4: An Exotic Energy Material. Nanomaterials. 2021;11:1286. doi: 10.3390/nano11051286. - DOI - PMC - PubMed
    1. Sai R., Arackal S., Kahmei R.D.R., Bhat N., Yamaguchi M., Shivashankar S.A. Crystallographic inversion-mediated superparamagnetic relaxation in Zn-ferrite nanocrystals. AIP Adv. 2020;10:4. doi: 10.1063/1.5130483. - DOI
    1. Cobos M.A., de la Presa P., Llorente I., Alonso J.M., Garcia-Escorial A., Marin P., Hernando A., Jimenez J.A. Magnetic Phase Diagram of Nanostructured Zinc Ferrite as a Function of Inversion Degree delta. J. Phys. Chem. C. 2019;123:17472–17482. doi: 10.1021/acs.jpcc.9b02180. - DOI
    1. Yafet Y., Kittel C. Antiferromagnetic Arrangements in Ferrites. Phys. Rev. 1952;87:290–294. doi: 10.1103/PhysRev.87.290. - DOI