On the Supervision of a Saturated SIR Epidemic Model with Four Joint Control Actions for a Drastic Reduction in the Infection and the Susceptibility through Time

Abstract

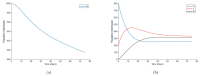
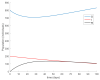
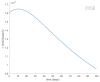
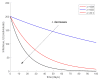
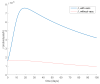
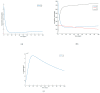
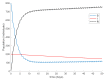
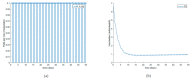
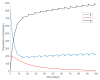
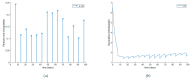
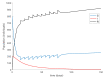
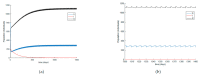
This paper presents and studies a new epidemic SIR (Susceptible-Infectious-Recovered) model with susceptible recruitment and eventual joint vaccination efforts for both newborn and susceptible individuals. Furthermore, saturation effects in the infection incidence terms are eventually assumed for both the infectious and the susceptible subpopulations. The vaccination action on newborn individuals is assumed to be applied to a fraction of them while that on the susceptible general population is of linear feedback type reinforced with impulsive vaccination actions (in practice, very strong and massive vaccination controls) at certain time points, based on information on the current levels of the susceptible subpopulation. Apart from the above vaccination controls, it is also assumed that the average of contagion contacts can be controlled via intervention measures, such as confinements or isolation measures, social distance rules, use of masks, mobility constraints, etc. The main objectives of the paper are the achievement of a strictly decreasing infection for all time periods and that of the susceptible individuals over the initial period if they exceed the disease-free equilibrium value. The monitoring mechanism is the combined activation of intervention measures to reduce the contagion contacts together with the impulsive vaccination to reduce susceptibility. The susceptibility and recovery levels of the disease-free equilibrium point are suitably prefixed by the design of the regular feedback vaccination on the susceptible subpopulation.

Keywords: SIR epidemic model; contact contagion rate; environment; equilibrium points; intervention measures; saturated incidence; vaccination controls.

Figure 1

(a) Evolution of the total population, and (b) each subpopulation according to model (1)–(3) with parameter values given by Table 1 and in the absence of external actions.

Figure 2

Evolution of the SIR model when λ = 0.9 is used in Equation (30) to determine the value of β.

Figure 3

Evolution of $\beta$ when it is selected using Equation (30) with λ = 0.9.

Figure 4

Evolution of the infectious subpopulation for different values of λ and β given by Equation (30).

Figure 5

Evolution of all of the subpopulations when a constant vaccination of 20% of the susceptible subpopulation is added to the control of the contagion rate. The value of β is given by Figure 3.

Figure 6

Vaccination applied when a constant term of the susceptible individuals is vaccinated (20%) and $\beta$ is given by Figure 3.

Figure 7

(a) Evolution of the system when $\beta$ is fixed through Equation (30) ($\lambda =0.9$) and a constant vaccination term of 20% of the susceptible individuals is also employed. (b) Detail of the simulation for the first 100 days.

Figure 8

(a) Vaccination function when $\beta$ is fixed through Equation (30) ($\lambda =0.9$) and a constant vaccination term of 20% of the susceptible individuals is also employed. (b) Detail of the simulation for the first 100 days.

Figure 9

Different values of β calculated through (30) corresponding to the application of constant vaccination and the absence of it.

Figure 10

Results obtained when vaccination of the newcomers is added to the control of the contagion rate and the constant vaccination to the susceptible subpopulation, (a) vaccination control, (b) populations, (c) transmission rate.

Figure 11

Evolution of all subpopulations when an impulsive vaccination of the susceptible individuals is added to the previous actions.

Figure 12

(a) Impulsive vaccination (everyday) and (b) total feedback vaccination applied.

Figure 13

Value of β obtained through (30) when only the contagion rate is applied and when all control actions are employed.

Figure 14

Evolution of all the subpopulations when an impulsive vaccination of susceptible individuals one day per week is added to the previous actions.

Figure 15

(a) Impulsive vaccination (once per week) and (b) total feedback vaccination applied.

Figure 16

Value of β obtained through (30) when the impulsive vaccination is applied once per week and every day.

Figure 17

Evolution of all the subpopulations when a variable impulsive vaccination of the susceptible individuals one day per week is added to the previous actions.

Figure 18

(a) Impulsive vaccination (once per week with time-varying amplitude) and (b) total feedback vaccination applied.

Figure 19

Evolution of all the subpopulations when a variable and limited-in-time impulsive vaccination of the susceptible individuals one day per week is added to the previous actions.

Figure 20

(a) Impulsive vaccination (once per week limited-in-time with time-varying amplitude) and (b) total feedback vaccination applied.

Figure 21

(a) Extended simulation time in Figure 14 and (b) zoomed image of the final time period for the susceptible and recovered individuals.

Figure 22

(a) Extended simulation time in Figure 19 and (b) zoomed image of the final time period for the susceptible and recovered individuals with limited-in-time impulsive vaccination effort.