Diffusion time dependence, power-law scaling, and exchange in gray matter

Abstract

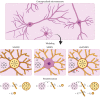
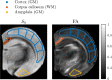
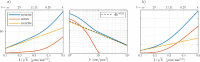
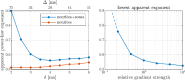
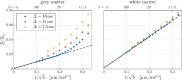
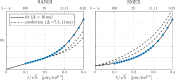
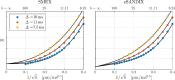
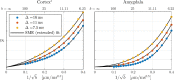
Characterizing neural tissue microstructure is a critical goal for future neuroimaging. Diffusion MRI (dMRI) provides contrasts that reflect diffusing spins' interactions with myriad microstructural features of biological systems. However, the specificity of dMRI remains limited due to the ambiguity of its signals vis-à-vis the underlying microstructure. To improve specificity, biophysical models of white matter (WM) typically express dMRI signals according to the Standard Model (SM) and have more recently in gray matter (GM) taken spherical compartments into account (the SANDI model) in attempts to represent cell soma. The validity of the assumptions underlying these models, however, remains largely undetermined, especially in GM. To validate these assumptions experimentally, observing their unique, functional properties, such as the b^-1/2 power-law associated with one-dimensional diffusion, has emerged as a fruitful strategy. The absence of this signature in GM, in turn, has been explained by neurite water exchange, non-linear morphology, and/or by obscuring soma signal contributions. Here, we present diffusion simulations in realistic neurons demonstrating that curvature and branching does not destroy the stick power-law behavior in impermeable neurites, but also that their signal is drowned by the soma signal under typical experimental conditions. Nevertheless, by studying the GM dMRI signal's behavior as a function of diffusion weighting as well as time, we identify an attainable experimental regime in which the neurite signal dominates. Furthermore, we find that exchange-driven time dependence produces a signal behavior opposite to that which would be expected from restricted diffusion, thereby providing a functional signature that disambiguates the two effects. We present data from dMRI experiments in ex vivo rat brain at ultrahigh field of 16.4T and observe a time dependence that is consistent with substantial exchange but also with a GM stick power-law. The first finding suggests significant water exchange between neurites and the extracellular space while the second suggests a small sub-population of impermeable neurites. To quantify these observations, we harness the Kärger exchange model and incorporate the corresponding signal time dependence in the SM and SANDI models.

Keywords: Diffusion MRI; Exchange; Gray matter; Microstructure; Soma and neurite density imaging; Standard model.

Fig. 1

Graphical representation of the considered models. The SANDI model represents the dMRI signal with sticks, spheres and an isotropic Gaussian component. These can tentatively be assigned to neurites, somas, and extracellular water. The SMEX model excludes spheres but includes exchange between the sticks and the isotropic Gaussian component. Two extensions to SMEX are considered: including spheres/somas and introducing a sub-population of sticks which do not exchange.

Fig. 2

Distant (left) and close (right) perspectives of the triangular surface mesh (prior to conversion to a tetrahedron volume mesh) for one example neuron visualized and generated using Blender and the Mcell team Blender addons.

Fig. 3

GM and WM ROIs superimposed on maps of signal magnitude at b = 0 (left) and fractional anisotropy (right) estimated from a DKI fit to the subset of data with b ≤ 3 ms/µm². The ROIs in cortex and corpus callosum are referred to as the GM and WM ROIs.

Fig. 4

The simulated signal as well as the separate soma and dendrite contributions for two combinations of pulse times: a) δ = 4.5 ms and Δ = 16 ms matching the experiment with the signal shown as a function of b^−1/2 (left) and in a double-log plot (middle) where the power-law shows as a straight line. b) δ = 13 ms and Δ = 30 ms matching those of (Veraart et al., 2020).

Fig. 5

The apparent power-law exponent for the neurite signal contribution (left) and the total neuron signal (right) as a function of pulse separation Δ for different pulse durations δ. The apparent exponent is here defined as the absolute value of the slope obtained from fitting to the log-log signal curve from b = 10 to 100 ms/µm².

Fig. 6

Left panel: Apparent power-law exponent for the neurite contribution and the total signal as functions of δ and Δ constrained by a target b = 100 ms/µm² with the employed scanner. Right panel: The lowest apparent exponent achievable (optimizing pulse times) as a function of available gradient strength relative to the employed scanner ($g_{max}$ = 3000 mT/m).

Fig. 7

Left: the GM signal at small b. Right: the corresponding mean diffusivity and kurtosis. Parameters were estimated for each diffusion time with DKI applied to the subset of data with b ≤ 3 ms/μm².

Fig. 8

The GM and WM signals at large b-values (ROIs given in Fig. 3). The black lines show linear fits to the subset of data with b ≥ 25 ms/µm² and Δ = 16 ms – lines are solid for b ≥ 25 ms/µm² and otherwise dashed.

Fig. 9

Both panels show the GM signal for Δ = 16 ms (ROI given in Fig. 2). Fits of SANDI (left) and SMEX (right) are shown with solid curves, while dashed curves show the predicted signal at Δ = 11 and 7.5 ms (using parameters obtained from the fitting). Parameter estimates are provided for completeness but note that the fits employed only the subset of data with Δ = 16 ms. For SANDI: $f_e$ = 64%, $D_e$ = 0.7 µm²/ms, $f_n$ = 17%, $D_n$ = 2.5 µm²/ms, $f_s$ = 19%, $R_s$ = 5.4 µm, and $f_{im}$ = 0. For SMEX: $f_e$ = 54%, $D_e$ = 0.6 µm²/ms, $f_n$ = 45%, $D_n$ = 1.9 µm²/ms, ${\tau }_n$ = 8.1 ms, and $f_{im}$ = 0.6%.

Fig. 10

Both panels show the GM signal (ROI given in Fig. 2). The curves show fits of SMEX (left) and eSANDIX (right). Parameter estimates are given in Table 1.

Fig. 11

Comparison of amygdala and a region of cortex (see Fig. 3– third sub-ROI from left). The curves show fits of SMEX extended with both somas and impermeable neurites. Parameter estimates for the cortex region: $f_e$ = 38%, $D_e$ = 0.8 μm²/ms, $f_n$ = 38%, $f_n^{\left(imp\right)}$ = 5%, $D_n$ = 0.6 μm²/ms, ${\tau }_n$ = 4.5 ms, $f_s$ = 20%, $R_s$ = 13.6 μm, $f_{im}$ = 0.5%. For amygdala: $f_e$ = 44%, $D_e$ = 0.8 μm²/ms, $f_n$ = 48%, $f_n^{\left(imp\right)}$ = 0.3%, $D_n$ = 0.6 μm²/ms, ${\tau }_n$ = 3.5 ms, $f_s$ = 7%, $R_s$ = 11.7 μm, $f_{im}$ = 0.5%.

Fig. A.1

The large-b GM signal from three supporting experiments on other brains. Data is shown with markers and fits of the SMEX and the extended SMEX (including somas and non-exchanging neurites) models are shown with solid and dashed curves respectively. In the case of specimen 2, only SMEX was fitted to the data.