An efficient algorithm for solving piecewise-smooth dynamical systems
- PMID: 35185303
- PMCID: PMC8816753
- DOI: 10.1007/s11075-021-01154-1
An efficient algorithm for solving piecewise-smooth dynamical systems
Abstract
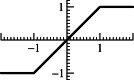
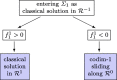
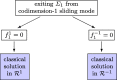
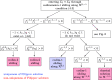
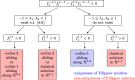
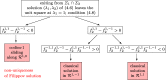
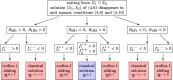
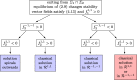
This article considers the numerical treatment of piecewise-smooth dynamical systems. Classical solutions as well as sliding modes up to codimension-2 are treated. An algorithm is presented that, in the case of non-uniqueness, selects a solution that is the formal limit solution of a regularized problem. The numerical solution of a regularized differential equation, which creates stiffness and often also high oscillations, is avoided.
Keywords: Codimension-2 manifold; Filippov solution; Hidden dynamics; Piecewise-smooth systems; Regularization; Scaling invariance.
© The Author(s) 2021.
Figures


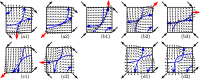
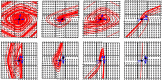
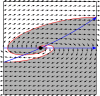
References
-
- Alexander JC, Seidman TI. Sliding modes in intersecting switching surfaces. I. Blending Houston J. Math. 1998;24(3):545–569.
-
- Brenan KE, Campbell SL, Petzold LR. Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations. Philadelphia: Classics in Appl. Math SIAM; 1996.
-
- Calvo M, Montijano JI, Rández L. Algorithm 968 DISODE45: A Matlab Runge-Kutta solver for piecewise smooth IVPs of Filippov type. ACM Trans. Math. Softw. 2017;43(3):Art. 25, 14. doi: 10.1145/2907054. - DOI
-
- Carver MB. Efficient integration over discontinuities in ordinary differential equation simulations. Math. Comput. Simulation. 1978;20(3):190–196. doi: 10.1016/0378-4754(78)90068-X. - DOI
-
- Den Hartog JP. Forced vibrations with combined viscous and coulomb damping. Philos. Mag. 1930;9(59):801–817. doi: 10.1080/14786443008565051. - DOI
LinkOut - more resources
Full Text Sources
