Reinforcement Learning Model With Dynamic State Space Tested on Target Search Tasks for Monkeys: Self-Determination of Previous States Based on Experience Saturation and Decision Uniqueness

Abstract

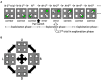
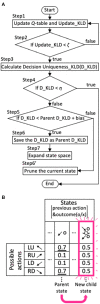
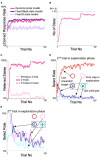
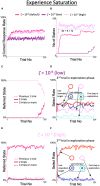
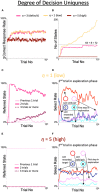
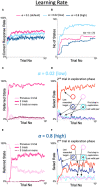
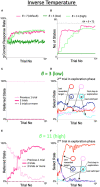
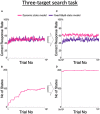
The real world is essentially an indefinite environment in which the probability space, i. e., what can happen, cannot be specified in advance. Conventional reinforcement learning models that learn under uncertain conditions are given the state space as prior knowledge. Here, we developed a reinforcement learning model with a dynamic state space and tested it on a two-target search task previously used for monkeys. In the task, two out of four neighboring spots were alternately correct, and the valid pair was switched after consecutive correct trials in the exploitation phase. The agent was required to find a new pair during the exploration phase, but it could not obtain the maximum reward by referring only to the single previous one trial; it needed to select an action based on the two previous trials. To adapt to this task structure without prior knowledge, the model expanded its state space so that it referred to more than one trial as the previous state, based on two explicit criteria for appropriateness of state expansion: experience saturation and decision uniqueness of action selection. The model not only performed comparably to the ideal model given prior knowledge of the task structure, but also performed well on a task that was not envisioned when the models were developed. Moreover, it learned how to search rationally without falling into the exploration-exploitation trade-off. For constructing a learning model that can adapt to an indefinite environment, the method of expanding the state space based on experience saturation and decision uniqueness of action selection used by our model is promising.

Keywords: decision uniqueness; dynamic state space; experience saturation; exploration-exploitation trade-off; indefinite environment; reinforcement learning; target search task.

Figure 1

Differences in the basic schemes between previous models and the model presented in the current study. (A) In the conventional reinforcement learning scheme, observed variables and state variables are not distinguished. That is, the current state s_i is set based on the observation of the environment o_{i, t−1} at the time t−1 and has a corresponding Q-table Q_i, which provides an action a_t. (B) In the partially observable Markov decision process (POMDP) model, the environment provides only a partial observation o_{?, t−1} to identify the current state. The agent has a set of beliefs or stochastic distribution for the possible states {b_i}, and renews them through actions a and their reward outcomes r. Note that similar to the conventional scheme, the possible states are provided to the POMDP model in advance, in the form of beliefs. (C) Our dynamic state scheme also hypothesizes that the agent receives only partial information from the environment. However, unlike POMDP, these observations are temporarily stored in working memory and serve to generate a new state not prepared a priori, based on the two criteria experience saturation and decision uniqueness.

Figure 2

Overview of the two-target search task. (A) Schematic of several trials before and after a valid pair change. The pair change triggers the transition from the exploitation phase to the exploration phase. Dashed lines, empty arrows and green spots denote valid pairs, gazes and correct targets, respectively. Note that the subjects were not instructed to move their eyes by the green spot before gaze shift. (B) Valid pairs are randomly altered after a series of correct trials.

Figure 3

Expansion and contraction of the state space. (A) Flowchart of the expansion and contraction process. (B) An example of state expansion derived from a parent state in Q-table. The direction of the arrow represents the target that the agent looked at, and o and x represent the correct answer and error, respectively. The example in the figure shows that a new state is generated from the state that the agent looked at LD and was rewarded one trial ago, to the state that it looked at LD and was rewarded one trial ago after it looked at RD and was rewarded two trials ago. The numbers in the Q-table represent Q-values. The initial Q-value for each action is set to 0.5.

Figure 4

Changes in the proposed model with learning. (A) Time course of the correct response rate and comparison with fixed state models. (B) Increase in the number of states. (C) Changes in the states referred to in each action selection. (D) Analysis of the model's behavior during the second trial of the exploration phase. “c” and “e” denote correct and error response, respectively. (E) Enlarged view of the 0–15% area of the select rate in (D).

Figure 5

Effects of threshold modulation of experience saturation. Formats are identical to Figure 4. (A) Correct response rates. (B) Corresponding number of states. (C,D) States referred to in each action selection (C) and analysis of the model's behavior in the second trial of the exploration phase (D) at a low value of ζ = 10⁻⁹. (E,F) Same plots as (C,D) for a high value of ζ = 10⁻³.

Figure 6

Effects of threshold modulation of the degree of decision uniqueness. Formats are identical to Figure 5. (A) Percentage of correct answers. (B) Changes in number of states. (C,D) States referred to in each action selection (C) and the model's behavior in the second trial of the exploration phase (D) at a low value of η = 1. (E,F) Same plots as (C,D) for a high value of η = 5.

Figure 7

Effects of modulation of learning rate. Formats are identical to Figures 5, 6. (A) Percentage of correct answers. (B) Changes in number of states. (C,D) States referred to in each action selection (C) and the model's behavior in the second trial of the exploration phase (D) at a low value of α = 0.02. (E,F) Same plots as (C,D) for a high value of α = 0.8.

Figure 8

Effects of modulation of inverse temperature in the softmax function used for action selection. Formats are identical to Figures 5–7. (A) Percentage of correct answers. (B) Changes in number of states. (C,D) States referred to in each action selection (C) and the model's behavior in the second trial of the exploration phase (D) at a low value of β = 3. (E,F) Same plots as (C,D) for a high value of β = 11.

Figure 9

Effects of the presence or absence of the parent–child comparison bias. (A,B) Percentage of correct answers (A), and changes in the number of states (B) in the two-target search task. (C,D) The same plots for the four-armed bandit task. The number in each circle in the inset of C represents the reward probability for each target. (E,F) The same plots for the alternative version of the four-armed bandit task. This version includes the two targets with the highest reward probabilities, as shown in the inset in (E).

Figure 10

Changes in the proposed model as it learned a three-target search task and comparison with the fixed 8by8-state model. (A) Correct response rate for the first 10⁵ trials. (B) Increase in the corresponding number of the states. (C) Correct response rate for the 9 × 10⁵th trial to the 10⁶th trial. (D) Corresponding number of states.

Figure 11

Comparison between the proposed model and the POMDP model. (A) Correct response rate in the two-target search task. (B,C) Correct response rates in the three-target search task for the first 10⁵ trials (B) and for the 9 × 10⁵th to the 10⁶th trials (C).

Figure 12

Comparison of the proposed model and the iHMMs in terms of the reproducibility of two-target search task learning. (A–C) Time courses of the correct response rate (A), increase in number of states (B), and increase in the cumulative number of target pair-switches (C) exhibited by the proposed model. (D–F) Identical plots of the Dirichlet process version of the iHMM (see Supplementary Figure 2C). (G) Changes in states with each action selection in the calculation example indicated by the filled arrows in (D–F). (H–J) Identical plots of the hierarchical Dirichlet process version of the iHMM (see Supplementary Figure 2D). (K) Plot identical to G for the calculation example indicated by the blank arrows in (H–J). The same color in the simulations of each model denotes the same calculation.

Figure 13

Analysis of the exploration–exploitation trade-off problem. (Left column) Amount of learning at the end of the last exploitation phase (abscissa) and the number of consecutive trials during which the model exhibited an action that persisted from the previous valid pair (ordinate). (Right column) Histograms of trials with perseveration as a percentage of the total number of trials. (A) Fixed 4-state model. (B) Fixed 8-state model. (C) Proposed model.